让我们计算矩阵的秩:
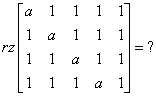
解决方案
你可以用几种方法来解决这个问题,最快的方法可能是将第五列乘以-1,然后加到第一、第二、第三和第四列,得到:
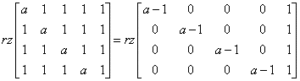 现在我们来看一下四阶矩阵的行列式:
现在我们来看一下四阶矩阵的行列式:
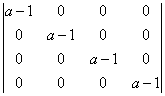 所有非主对角线元素都为零的行列式等于主对角线元素的乘积(总有一天我会证明这一点 🙂 ),所以:
所有非主对角线元素都为零的行列式等于主对角线元素的乘积(总有一天我会证明这一点 🙂 ),所以:
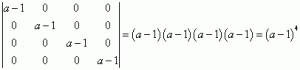 这个行列式在所有a不等于1时都不为零。因此,对于这样的a,我们要计算的矩阵的秩是4(因为可以从中提取非零的四阶小矩阵,而无法得到更大的)。
这个行列式在所有a不等于1时都不为零。因此,对于这样的a,我们要计算的矩阵的秩是4(因为可以从中提取非零的四阶小矩阵,而无法得到更大的)。
当 ![]() 时会怎样呢?此时我们得到的矩阵秩(将a替换为1):
时会怎样呢?此时我们得到的矩阵秩(将a替换为1):
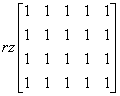 这个秩为1(例如,你可以再次用第五列作用于其余列并消去零列)。
这个秩为1(例如,你可以再次用第五列作用于其余列并消去零列)。
因此,当a不等于1时,矩阵的秩为4,当a等于1时,矩阵的秩为1。


