我们有一个函数的极限:
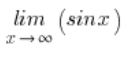
直观上我们感觉上面的极限是不存在的。x 变得越来越大,而正弦值一直在 -1 和 1 之间“摆动”。
正式证明
但如何正式地展示并证明这一点呢?
根据定义当 x 趋向无穷大时的函数极限,我们知道极限存在,如果对于 每一个趋向 ![]() 的自变量序列,对应的函数值序列都收敛于同一个数(那么这个数就是极限)。
的自变量序列,对应的函数值序列都收敛于同一个数(那么这个数就是极限)。
所以为了展示这样的极限不存在,只需取两个任意趋向 ![]() 的自变量序列,并展示对应的函数值序列收敛于两个不同的数。
的自变量序列,并展示对应的函数值序列收敛于两个不同的数。
我们知道正弦函数是周期性的,因此可以取如下序列:
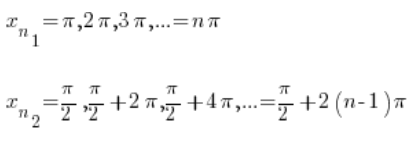
显然,当 ![]() 时,这两个序列都趋向于无穷大。
时,这两个序列都趋向于无穷大。
现在我们来看这些序列对应的函数值序列 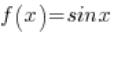 :
:
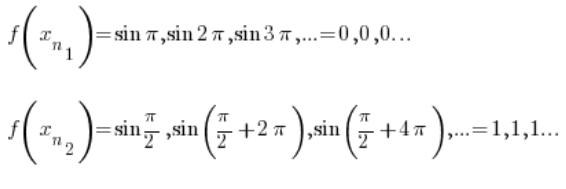
显然,第一个序列收敛于 0,第二个序列收敛于 1。
这足以证明函数的极限:
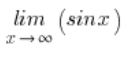
不存在。


