假设我们将 矩阵的秩 定义为：“矩阵中线性独立的行和列的数量”。从这个定义一开始就可以得出哪些性质？
首先，很明显 矩阵的秩 可以是：1，或者4，或者有时是0。但肯定不会是：-4，或者 
。
但这就是全部吗？我们来看一个矩阵的例子：
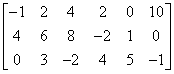
这个矩阵有3行6列。
我们问自己，这个矩阵的 秩 可能是多少？它可以等于7吗？显然不可能，因为既然 矩阵的秩 是“线性独立的行和列的数量”，在这种情况下不可能是7，因为这个矩阵既没有这么多行，也没有这么多列！
现在一个更难的问题…… 秩 可以是6吗？毕竟这个矩阵有6列……
答案是否定的。6必须是“线性独立的行和列的数量”。6可以是线性独立的列的数量（因为它有6列），但不能是线性独立的行的数量（因为它只有3行）。而它应该是线性独立的“行和列”的数量。
所以，很明显这个 矩阵的秩 最大可以是3。
我们得出一个有用的性质：
秩(A) <= 最小值(矩阵的行数, 矩阵的列数)
因此，通过观察矩阵，可以立即知道它的 最大秩 – 这有时非常有用。
konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.
Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.
Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.
Wirtualny nauczyciel AI działający w przeglądarce internetowej.
