用定积分计算的椭球体体积（但不是旋转椭球体，而是那种野生的）

---

我们来说说如何计算椭球体的体积：

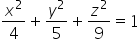
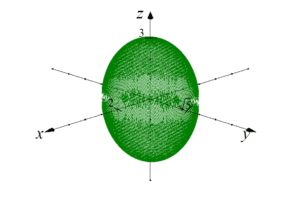
这是一个椭球体，它在x, y, z轴上的交点分别是2, 和3 (椭球体的一般方程是: 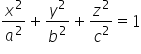, 其中a,b,c是交点坐标).

这不是一个旋转椭球体，不是通过任何曲线绕任何轴旋转生成的，我们不能用标准的旋转体积公式来解决:

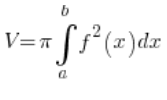
我们得另想办法。

1. 我们在椭球体的中心和OZ轴上取一个任意点M(z)。

通过这个点并垂直于OZ轴的平面“切割”出一个椭圆：

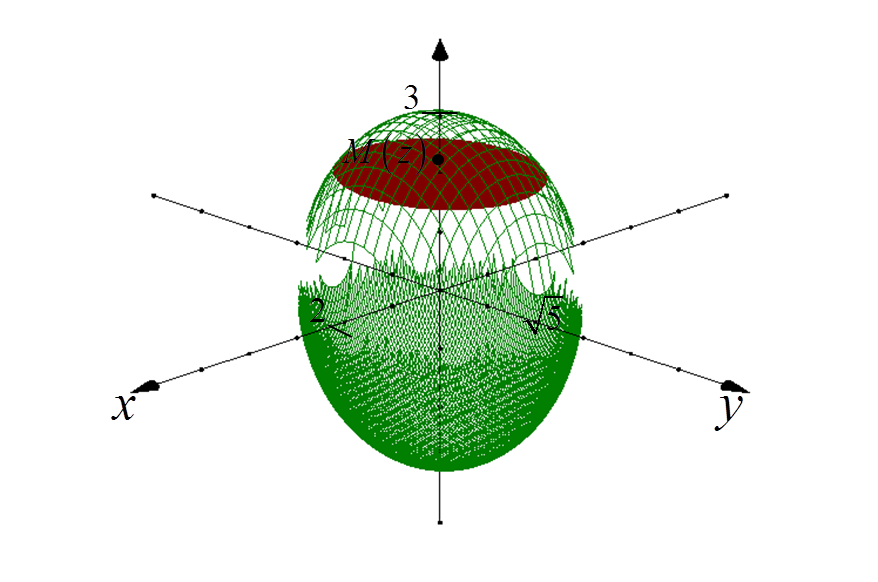
2. 我们确定在XY平面上的椭圆“切割”投影方程

我们从椭球体的一般方程中确定这个椭圆的方程，对于固定的’z’ (我们把’z’当作常数):

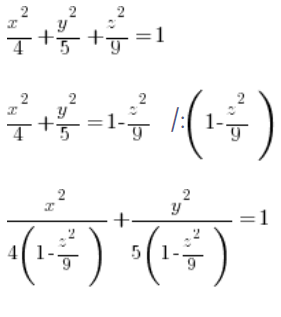
显然，我们的一般椭球体方程中的’a’和’b’ (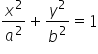) 是:

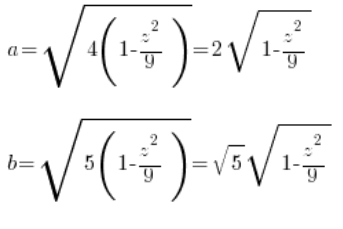
4. 根据变量’z’计算这个截面的面积

这个椭圆的面积取决于所选的’z’点，也就是说它是一个关于’z’的函数。我们可以用椭圆面积的现成公式来计算():

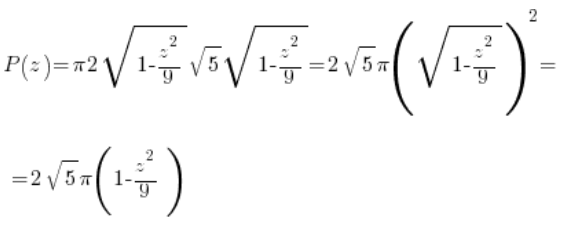
或者费力地计算适当的定积分（当然使用椭圆的参数形式和公式来计算参数形式的面积）:

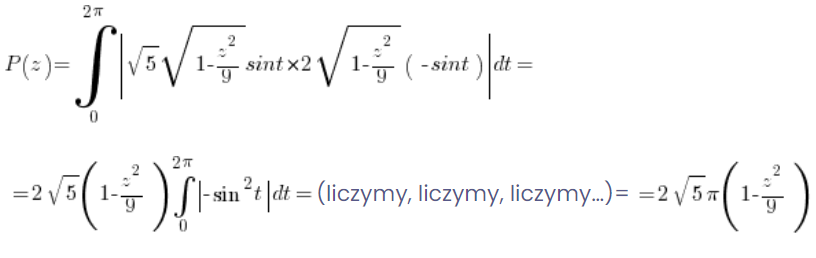
5. 用截面积计算体积

现在是关键时刻。体积等于——这听起来不太好——所有截面的“和”（即积分），大致来说：

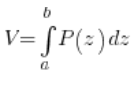
其中 是截面积关于OZ轴的函数，’a’和’b’是’z’的变化范围。

也就是说：

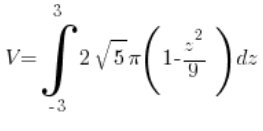=（算，算，算…）=

这与椭球体的一般公式一致().

结束

值得记住这个一般的思路，特别是，复杂的、非旋转体的体积可以通过积分其截面积函数来计算。