欧拉第三类替换 – 总结

---

欧拉替换 I、II、III 类 – 不再需要更多

在之前的帖子中，我展示了如何在以下类型的积分中使用欧拉替换：

• 欧拉替换 I 类 (当 a>0)
• 欧拉替换 II 类 (当 c>0)

在这篇文章中，我们将讨论第三种也是最后一种欧拉替换，当积分中的：

二次多项式 , 有两个不同的根 , 也就是说，当它的 , 即当它可以写成乘积形式时： .

但是，在我们开始之前，让我们注意到这三种情况：

• I 类，当 a>0
• II 类，当 c>0
• III 类，当有两个不同的根时

将使我们能够解决任何类型的积分：

事实上，I 类和 III 类就足够了。

为什么？

因为当 我们可以忽略它，因为二次多项式 变成了线性形式 , 我们可以用比欧拉更简单的替换来解决。

那么当 a<0 (不适合 I 类) 且二次多项式只有一个或根本没有根 (不适合 III 类) 时怎么办？

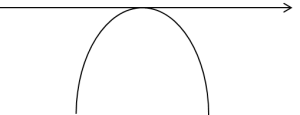
那么它的图形会是这样的（记得中学的 – 开口向下）：

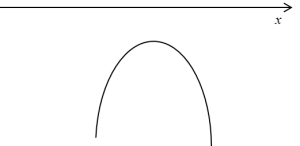
或者，如果根本没有根，那么会是这样的：

这有什么启示？在这两种情况下，二次多项式将取负值（最多只有一个点除外），我提醒你，我们在计算积分：

也就是说，被积函数中的二次多项式在根号下，而根号不能从负值中计算出来（当然，我们在玩实数）。也就是说，这样的函数的定义域最多只有一个点，也就是说完全没有意义，我们肯定不会得到这样的例子。除非教授在编写测验例题时非常疲倦。

因此，可以忽略 a<0 且二次多项式 没有两个根的情况，现在显然 I 类和 III 类欧拉替换适用于任何类型的积分：

那么，让我们开始第三种欧拉替换。

欧拉替换 III 类

我们有一个积分：

,

其中 有 , 也就是说可以写成：

,

其中 是它的根。

我们在这里使用的替换是：

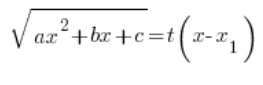
我们将这个替换平方，两边的二次多项式写成乘积形式（我们知道可以），将两边除以 并继续像之前的替换一样，依次确定：

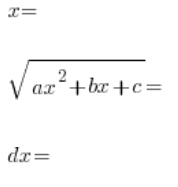
最后我们将整个过程代入初始积分，结果是一个通常比较繁琐的有理积分。

开始吧。

例子

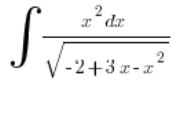
我们的 (也就是说 a<0，也就是说不使用 I 类替换)，我们的 (也就是说 c<0，也就是说不使用 II 类替换)，但我们的 ，所以我们可以使用 III 类替换。

首先计算 ：

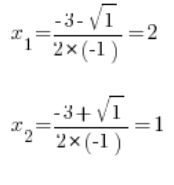
使用欧拉 III 类替换：

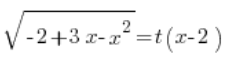
平方两边：

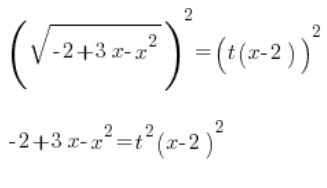
将左边的二次多项式写成乘积形式（记住这里的 !!!）：

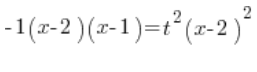
将两边除以 ：

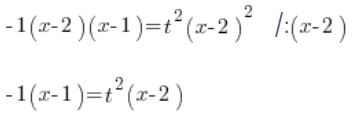
确定 ：

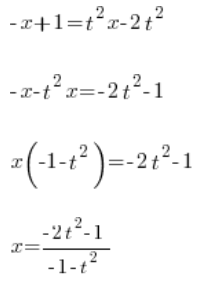
我们有了 使用变量 确定的。现在我们来确定 。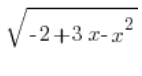

回到我们的第一个替换，我们有：

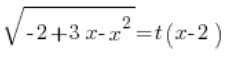
插入确定的 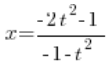，我们得到：

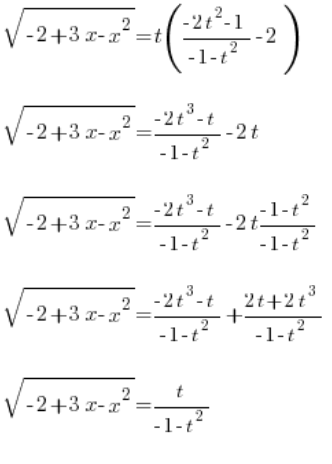
我们有了漂亮的 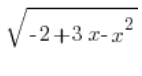确定的。现在只剩下 ，我们通过求 的导数来计算：

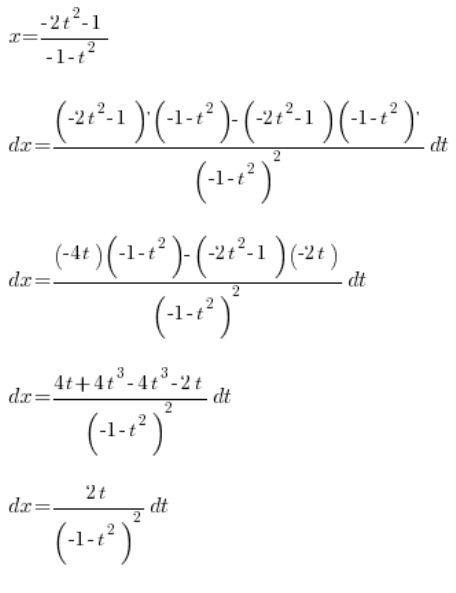
所以我们有了：

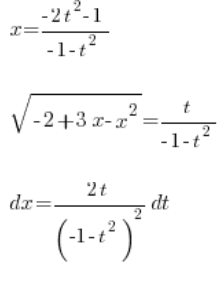
，一切使用变量 。我们将其插入积分中：

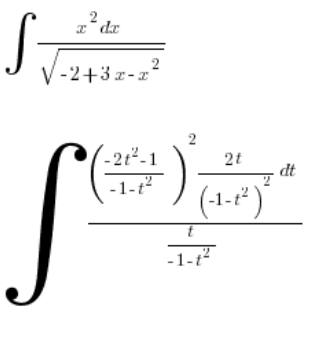
简化：

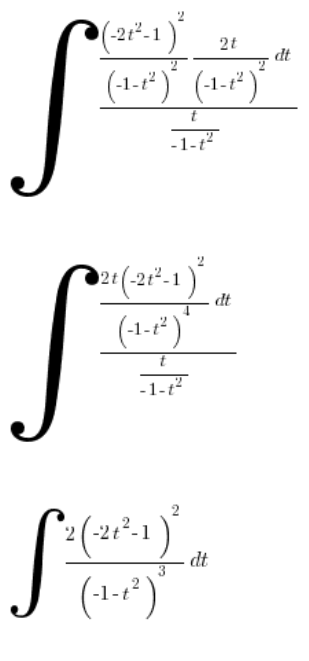
如预期，我们得到一个非常复杂的有理积分，我不会计算。

最后，值得注意的是…

关于欧拉替换的注意事项

我们有一个积分：

  ,

其中：

• I 类，当 a>0
• II 类，当 c>0
• III 类，当有两个不同的根时

显然，经常可以用欧拉替换中的一个或甚至任意一个来解决（当 a>0，c>0 并且同时 ）。

没问题，虽然由于计算的简便性，我建议优先使用 I 类，如果不行，则使用 II 类，如果还不行，则使用 III 类。

关于欧拉替换的内容就这么多，希望对你的学习有所帮助，欢迎在帖子下方留言讨论。