Currently Empty: zł0.00
Krystian Karczyński- 24 7 月 2024
- Comment 0
在我的复数课程中，我展示了一种方法，通过向已经存在的两个方程组中添加第三个方程，从而极大地简化和缩短了进一步的计算过程。
我展示了这个方法，但没有任何解释。
最近我收到了一个邮件，内容如下：
你好
您能解释一下为什么我们在计算复数的平方根时可以使用添加第三个方程的方法吗？
x^2 + y^2 = 我们要计算平方根的数的模
这是一个非常好的问题，真正的数学祝福那些不相信教授的话的人，而是总是问：“这是从哪里来的？” 🙂
解释
那么现在我只剩下用一种可能的方式来解释这个方法了：
在计算平方根的前几步后，我们有这样的情况：
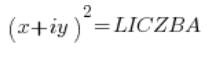
由于左边和右边的数（每次都不再写“复数”了）是相等的，所以它们的模也必须相等（反过来则不成立，但这不重要），即：
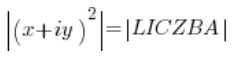
平方数是数乘以数，即：
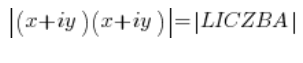
复数的模有个特性：
，所以在左边我们可以写：
…然后在左边计算模，我们有：
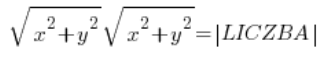
即：
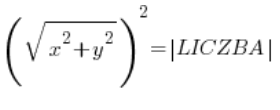
即：
即：
成功
感谢这个好问题！
