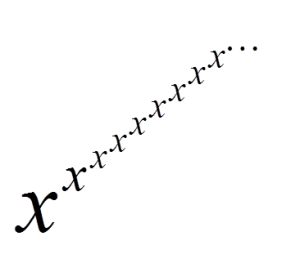Currently Empty: zł0.00
Krystian Karczyński- 7 8 月 2024
- Comment 0
作为一个趣闻，我将计算函数的极限：
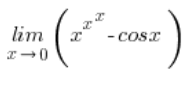
比计算本身更有趣的是可以从中得出的两个教训。但教训在最后（有人见过开头就有教训的故事吗）？ 现在我来计算：
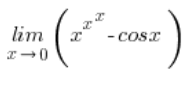
一开始，我看看情况如何，然后我有：
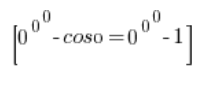
也就是说，我不知道情况如何，因为我甚至不知道 
结果如何 (这是一个未定义的符号)，更不用说像这样的怪东西了： 
.
然而，似乎余弦函数没有问题，所以我在旁边计算，看看单独情况如何：
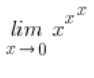
我会使用洛必达法则 (我在我的课程中详细解释了这一点)，也就是说，我会使用公式 (
):
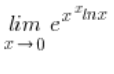
但情况还是不好，因为在指数上还有未定义的符号 
，所以我第二次转换它：
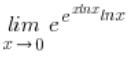
现在我可以放心地开始工作了。我在旁边计算：
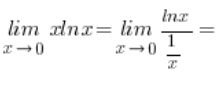
，所以我有未定义的符号 
所以我用洛必达法则：
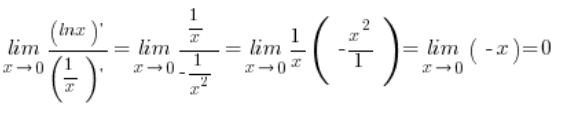
也就是说，我在旁边计算出：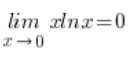 
.
所以，回到极限：
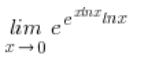
我现在知道我处于这种情况：
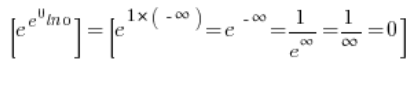
也就是说，结果是：
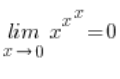
所以整个极限是：
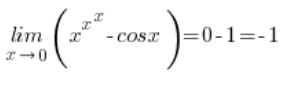
而余弦函数只是吓唬人而已。
这故事的教训
有两个。
- 在更难的极限中，总是可以而且有时必须取其一部分并计算其“在旁边”的趋势。
- 有时公式中的某些部分可能像这个余弦函数一样被添加进来。结果发现我不需要对它做任何处理，只需在最后代入零。
