两种不连续点（函数极限）
Krystian Karczyński
eTrapez网站的创始人兼负责人。
波兹南理工大学（波兰）数学专业硕士。拥有多年数学家教经验。创建了第一个eTrapez课程，这些课程在波兰全国的学生中获得了巨大的流行。
居住在什切青（波兰）。喜欢森林散步、海滩放松和划独木舟。
函数在一点的连续性
如我们所知（即使只是从我的极限课程中），函数 
在点 
处是连续的，当：
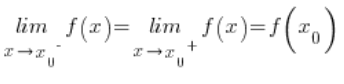
也就是说，当函数在这一点的左极限等于右极限等于这一点的函数值时，函数在这一点是连续的。
如果这些等式中的任何一个不成立，那么函数 在点 处不连续，这一点被称为不连续点。
在这个命名中，我们可以更进一步区分不连续点。我们这样做：
第一类不连续点
当 点称为第一类不连续点时，如果极限 
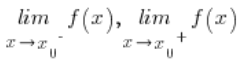是有限的（即它们是数字）。
另外，如果这些极限是相等的，那么这个第一类不连续点称为可去除的。
第二类不连续点
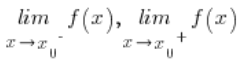当 点称为第二类不连续点时，如果极限 不是有限的（即它们等于正无穷或负无穷）。
例子 1
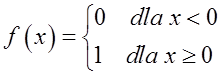
这个函数在 
点处有一个不连续点（因为这一点的左极限等于 0，右极限等于 1）。这是一个第一类不连续点，因为这一点的左极限和右极限是有限的（0 和 1）。这不是一个可去除的第一类不连续点，因为极限不相等。
例子 2
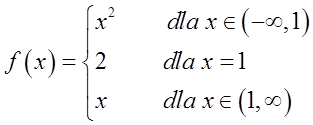
这个函数在 
点处有一个不连续点（因为这一点的左极限和右极限不等于这一点的函数值）。这是一个第一类不连续点，因为这一点的左极限和右极限是有限的（等于 1）。这是一个可去除的第一类不连续点，因为左极限和右极限相等。
例子 3
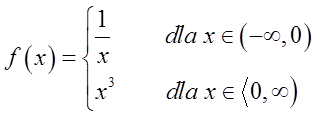
这个函数在 点处有一个不连续点（因为这一点的左极限和右极限不相等）。这是一个第二类不连续点，因为这一点的左极限等于 
。
你在寻找大学或高中级别的数学家教吗？ 或者你需要一个课程来帮助你准备高考吗？
我们是eTrapez团队。我们以清晰、简单和非常详细的方式教授数学 - 甚至可以触及到最抗拒学习的人。
我们创建了用易懂的语言解释的视频课程，可以下载到电脑、平板或手机上。你只需打开视频，就像在家教课上一样，观看和聆听。无论是白天还是夜晚，任何时候都可以。
