Currently Empty: zł0.00
Krystian Karczyński- 28 6 月 2024
- Comment 0
在 有理不定积分中，如我们所知，经常需要将被积函数的分母分解为因式，并进一步分解为简单分数。
然而，仅仅是因式分解就可能经常是个麻烦。
典型情况
对于简单的情况，例如：
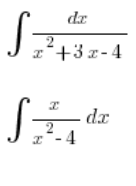
我们可以应对：
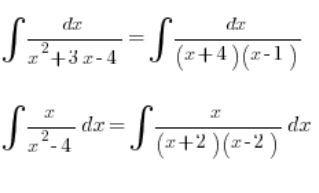
如果分母中有一个适当排列的三次多项式，我们也能应对：
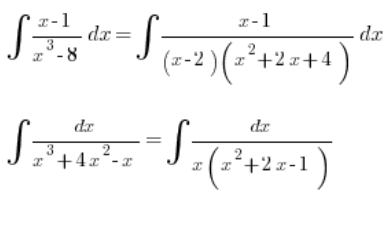
分母中的不友好的三次多项式
问题开始于分母中有一个更难以分解的三次多项式，例如：
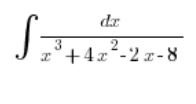
深呼吸。
控制住恐慌。
这种事情（这种多项式的因式分解）在高中就已经做过了，而且是基础水平的。
只需要一个聪明的小技巧：
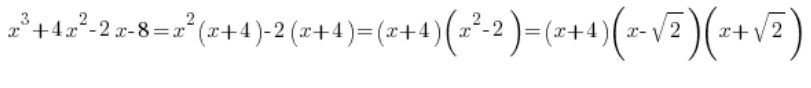
还记得吗？当然记得…
因此我们可以分解分母中的多项式：
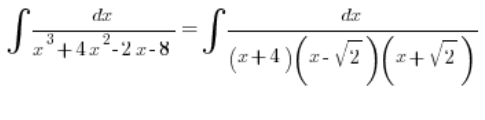
然后按照规则分解为三个简单分数。
更难的因式分解
那这样的情况呢？还记得高中学的（这已经是扩展范围了）吗？
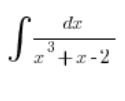
这里有点更糟糕。中间的项需要拆分为两个：
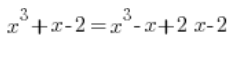
然后按照老方法继续：
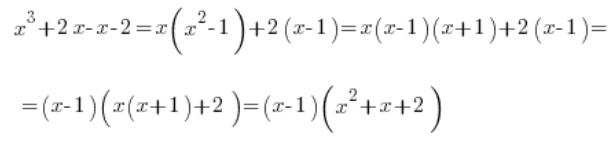
也就是说，积分应写为：
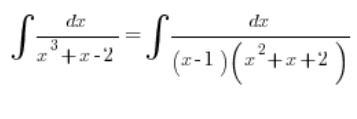
然后继续计算。
有理积分中分母的因式分解方法
总的来说，记住在有理积分中，如果需要将多项式分解为因式，所有的高中技巧都是允许的，可能还包括例如：
- 通过辅助置换分解一些四次多项式
- “盲目”寻找根，并分解多项式以降低其阶数
当然，我们现在只谈论更难的有理不定积分，这些积分在许多（大多数？）大学甚至没有引入！
