Wzory na pochodne
Temat: Właściwości pochodnych. Wyprowadzenie właściwości pochodnych.
Streszczenie
Jak wiemy, istnieją reguły dotyczące obliczania pochodnej z dodawania, odejmowania, mnożenia, dzielenia i mnożenia funkcji:
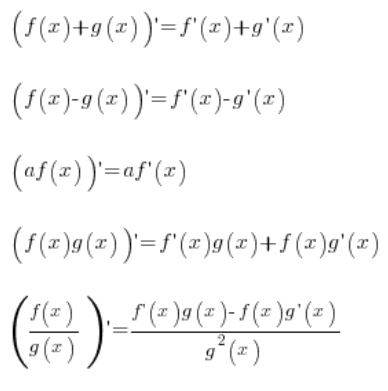
Pozwalają one obliczać pochodne już z bardziej złożonych stworów matematycznych, takich jak:
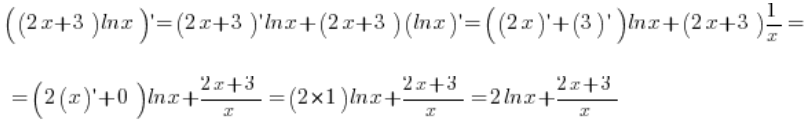
Na tym wykładzie wyprowadzimy sobie wszystkie właściwości pochodnych, jedna po drugiej, z samej definicji pochodnej 🙂
1.  – pochodna dodawania
– pochodna dodawania
Weźmy funkcję składającą się z sumy dwóch innych funkcji: ![]() . Trzeba pokazać, że pochodna z takiej funkcji równa jest sumie pochodnych z funkcji f i g. Zakładamy, że funkcje f i g mają pochodne w punkcie x.
. Trzeba pokazać, że pochodna z takiej funkcji równa jest sumie pochodnych z funkcji f i g. Zakładamy, że funkcje f i g mają pochodne w punkcie x.
Z definicji pochodna funkcji u w punkcie x wynosi:
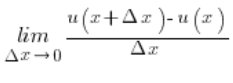
![]() obliczymy, wstawiając do wzoru na u(x):
obliczymy, wstawiając do wzoru na u(x): ![]() wszędzie w miejsce x-sa
wszędzie w miejsce x-sa ![]() , czyli:
, czyli:
![]()
Wzór na ![]() mamy z założenia, zatem:
mamy z założenia, zatem:
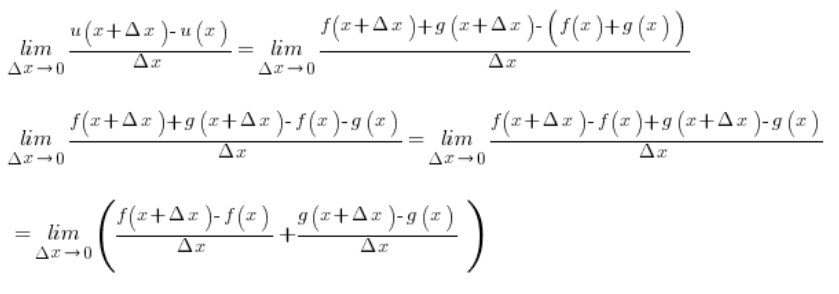
Pierwszy składnik to pochodna funkcji f w punkcie x z definicji (przy ![]() ), a drugi składnik to pochodna funkcji g w punkcie x z definicji. Założyliśmy, że obie te pochodne istnieją, zatem można zapisać, że:
), a drugi składnik to pochodna funkcji g w punkcie x z definicji. Założyliśmy, że obie te pochodne istnieją, zatem można zapisać, że:
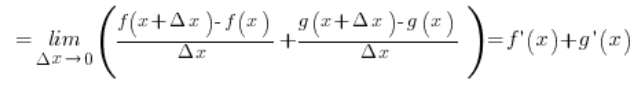
Udowodniliśmy w ten sposób naszą własność.
2.  – pochodna odejmowania
– pochodna odejmowania
Weźmy funkcję składającą się z różnicy dwóch innych funkcji: ![]() . Trzeba pokazać, że pochodna z takiej funkcji równa jest różnicy pochodnych z funkcji f i g. Zakładamy, że funkcje f i g mają pochodne w punkcie x.
. Trzeba pokazać, że pochodna z takiej funkcji równa jest różnicy pochodnych z funkcji f i g. Zakładamy, że funkcje f i g mają pochodne w punkcie x.
Z definicji pochodna funkcji u w punkcie x wynosi:
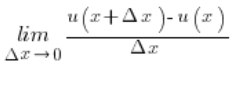
![]() obliczymy, wstawiając do wzoru na u(x):
obliczymy, wstawiając do wzoru na u(x): ![]() wszędzie w miejsce x-sa
wszędzie w miejsce x-sa ![]() , czyli:
, czyli:
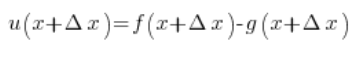
Wzór na ![]() mamy z założenia, zatem:
mamy z założenia, zatem:
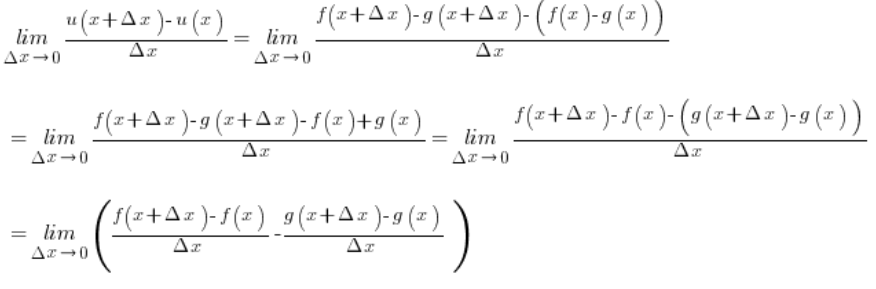
Pierwszy składnik to pochodna funkcji f w punkcie x z definicji (przy ![]() ), a drugi składnik to pochodna funkcji g w punkcie x z definicji. Założyliśmy, że obie te pochodne istnieją, zatem można zapisać, że:
), a drugi składnik to pochodna funkcji g w punkcie x z definicji. Założyliśmy, że obie te pochodne istnieją, zatem można zapisać, że:
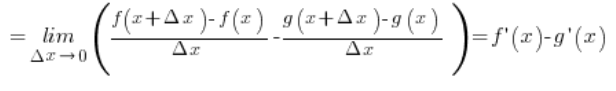
Udowodniliśmy w ten sposób naszą własność.
Uogólnienie własności 1. i 2.
Własności 1. i 2. można łatwo uogólnić na przypadek sumy/różnicy nie tylko dokładnie dwóch funkcji, ale sumę/różnicę dowolnej 'n’ liczby funkcji:
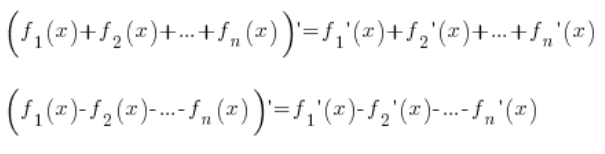
Postępujemy analogicznie, jak dowodząc przypadku dwóch zmiennych, bralibyśmy:
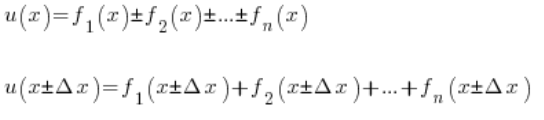
3.  – wyłączanie stałej przed nawias
– wyłączanie stałej przed nawias
Weźmy funkcję składającą się ze stałej przemnożonej przez inną funkcję: ![]() . Trzeba pokazać, że pochodna z takiej funkcji równa jest stałej c przemnożonej przez funkcję f. Zakładamy, że funkcja f ma pochodną w punkcie x.
. Trzeba pokazać, że pochodna z takiej funkcji równa jest stałej c przemnożonej przez funkcję f. Zakładamy, że funkcja f ma pochodną w punkcie x.
Z definicji pochodna funkcji u w punkcie x wynosi:
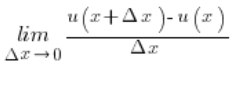
![]() obliczymy, wstawiając do wzoru na u(x):
obliczymy, wstawiając do wzoru na u(x): ![]() wszędzie w miejsce x-sa
wszędzie w miejsce x-sa ![]() , czyli:
, czyli:
![]()
Wzór na ![]() mamy z założenia, zatem:
mamy z założenia, zatem:
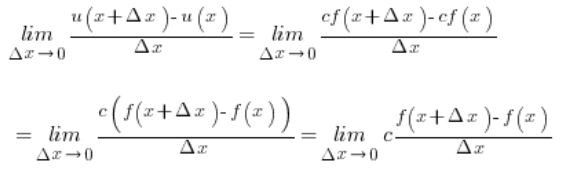
Ułamek w wyrażeniu to pochodna funkcji f w punkcie x z definicji (przy ![]() ). Założyliśmy, że ta pochodne istnieje, zatem można zapisać, że:
). Założyliśmy, że ta pochodne istnieje, zatem można zapisać, że:
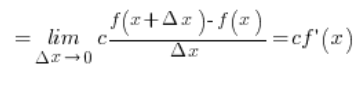
Własność jest więc udowodniona.
4.  – pochodna z mnożenia
– pochodna z mnożenia
Bierzemy funkcję składającą się z mnożenia dwóch innych funkcji: ![]() . Trzeba pokazać, że pochodna z takiej funkcji równa jest pochodnej z funkcji f pomnożonej przez funkcję g plus funkcja f przemnożona przez funkcję g . Zakładamy, że funkcje f i g mają pochodne w punkcie x.
. Trzeba pokazać, że pochodna z takiej funkcji równa jest pochodnej z funkcji f pomnożonej przez funkcję g plus funkcja f przemnożona przez funkcję g . Zakładamy, że funkcje f i g mają pochodne w punkcie x.
Z definicji pochodna funkcji u w punkcie x wynosi:
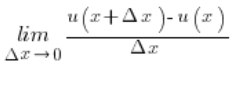
W dowodzie tej własności dogodnie będzie przyjąć trochę inne oznaczenia, niż stosowaliśmy do tej pory – dla czytelności zapisu. Jest to zarazem świetny test dla Ciebie – czy rozumiesz rzeczywiście o co chodzi z tą definicją pochodnej, czy tylko skułeś wzorek na pamięć i umiesz do niego podstawić.
We definicji pochodnej z funkcji u mamy wyrażenie: ![]() . Zauważmy, że TO SAMO (wartość funkcji u w punkcie x powiększonym o przyrost
. Zauważmy, że TO SAMO (wartość funkcji u w punkcie x powiększonym o przyrost ![]() można zapisać INACZEJ:
można zapisać INACZEJ:
![]() – czyli jako wartość funkcji u w punkcie x powiększonej o pewien przyrost wartości funkcji u.
– czyli jako wartość funkcji u w punkcie x powiększonej o pewien przyrost wartości funkcji u.
ZATRZYMAJ SIĘ TUTAJ – JEŚLI TEGO NIE ZROZUMIESZ NIE IDŹ DALEJ 🙂
Wiemy, że jeśli z założenia ![]() , to:
, to:
![]()
Korzystając z naszych zmienionych oznaczeń (można je zastosować także do funkcji f i funkcji g):
![]()
Z założenia ![]() – korzystam z tego po lewej stronie, a po prawej stronie przemnażam nawiasy i mam:
– korzystam z tego po lewej stronie, a po prawej stronie przemnażam nawiasy i mam:
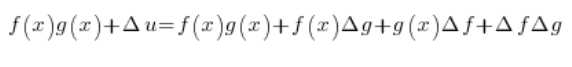
Po skróceniu:
![]()
Zauważmy teraz, że wracając do naszej pochodnej, którą mamy policzyć z definicji:
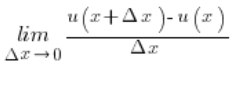
Wyrażenie w liczniku: ![]() jest to dokładnie nasz przyrost wartości
jest to dokładnie nasz przyrost wartości ![]() , bo przyrost wartości to wartość w punkcie powiększonym o przyrost pomniejszona o wartość w punkcie „wyjściowym”. Również konieczne jest tutaj, żebyś się zatrzymał, ewentualnie wrócił do definicji pochodnej, żeby zrozumieć, dlaczego:
, bo przyrost wartości to wartość w punkcie powiększonym o przyrost pomniejszona o wartość w punkcie „wyjściowym”. Również konieczne jest tutaj, żebyś się zatrzymał, ewentualnie wrócił do definicji pochodnej, żeby zrozumieć, dlaczego:
![]()
I w konsekwencji:
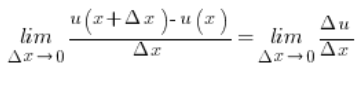
![]() policzyliśmy parę linijek wyżej:
policzyliśmy parę linijek wyżej:
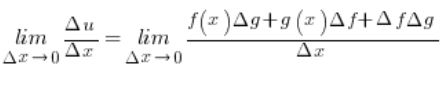
Czyli:
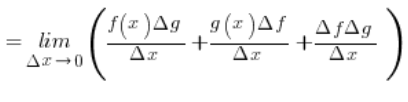
Przyrosty wartości funkcji f ![]() i funkcji g
i funkcji g ![]() równe są odpowiednio (zgodnie z naszymi oznaczeniami):
równe są odpowiednio (zgodnie z naszymi oznaczeniami):
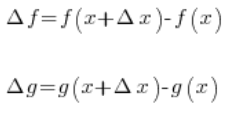
Mamy zatem granicę:
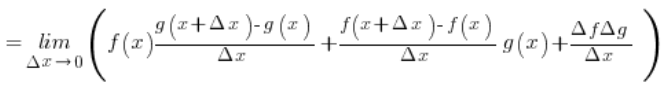
Zauważmy, że w pierwszych dwóch składnikach mamy pochodne funkcji f i g z definicji (założyliśmy, że istnieją) – a co z trzecim składnikiem? Rozpiszmy go trochę na boczku:
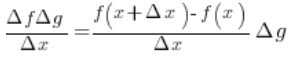
Mamy więc pochodną funkcji f w punkcie x (jakąś wartość) pomnożoną przez coś dążącego do zera (przyrost wartości g ![]() dąży oczywiście do zera przy
dąży oczywiście do zera przy ![]() ), czyli całość zbiega do zera.
), czyli całość zbiega do zera.
Trzeci składnik więc w wyrażeniu:
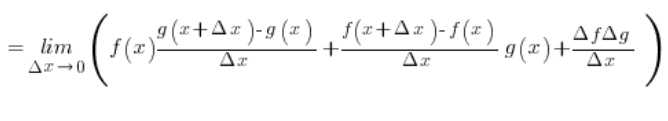
…zbiega do zera i mamy:
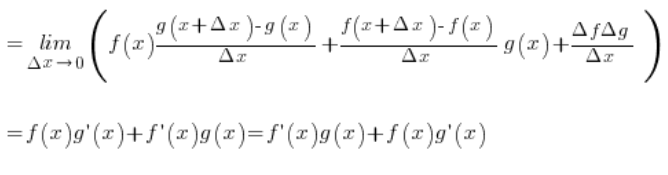
…czego należało dowieść.
5.  – pochodna z dzielenia
– pochodna z dzielenia
Bierzemy funkcję składającą się z mnożenia dwóch innych funkcji: 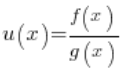 . Trzeba pokazać, że pochodna z takiej funkcji równa jest funkcji jak we wzorze . Zakładamy, że funkcje f i g mają pochodne w punkcie x, oraz, że funkcja g jest przyjmuje wartość różną od zera w punkcie, w którym liczymy pochodną.
. Trzeba pokazać, że pochodna z takiej funkcji równa jest funkcji jak we wzorze . Zakładamy, że funkcje f i g mają pochodne w punkcie x, oraz, że funkcja g jest przyjmuje wartość różną od zera w punkcie, w którym liczymy pochodną.
Z definicji pochodna funkcji u w punkcie x wynosi:
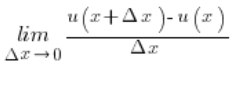
Mamy:
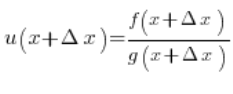
Przechodząc na inne oznaczenia, stosowane w wykazywaniu wzoru na pochodną z mnożenia:
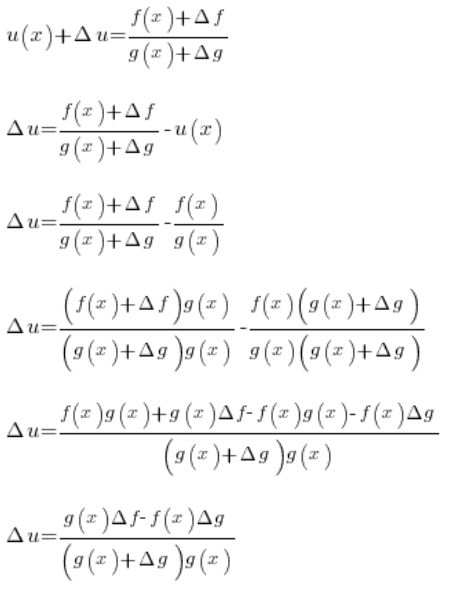
A jak wiemy z punktu 4. można zapisać:
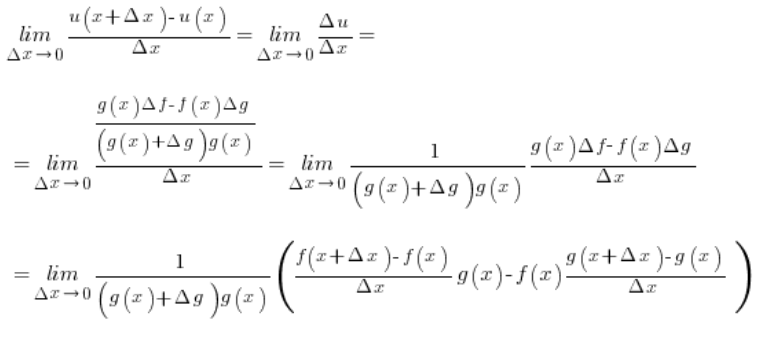
Składniki w nawiasie to pochodne funkcji f i g z w punkcie x z definicji. ![]() przy
przy ![]() , mamy zatem wzór:
, mamy zatem wzór:
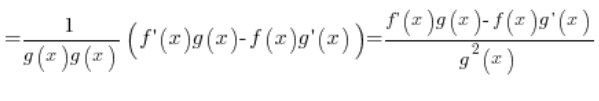
Co należało wykazać 🙂
KONIEC
Kliknij, aby zobaczyć, jak udowodnić można wzór na pochodną funkcji złożonej (następny Wykład) –>

 – pochodna odejmowania
– pochodna odejmowania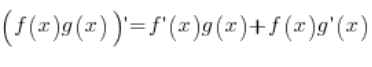 – pochodna z mnożenia
– pochodna z mnożenia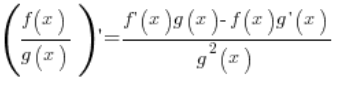 – pochodna z dzielenia
– pochodna z dzielenia
Dave
Zastosowanie rachunku różniczkowego funkcji jednej zmiennej.
Jak się zabrać za udowadnianie nierówności?
Np.: Pokazać, że 2lnx1?