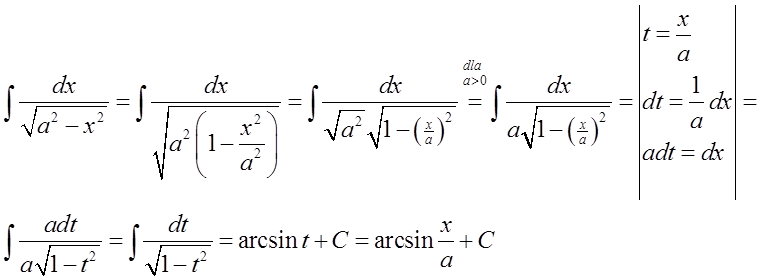Професори в університетах мають свої вимоги. Багато з них – для блага своїх студентів, звичайно – не вагаються детально визначити правила, за якими мають розв’язуватися задачі.
Професори в університетах мають свої вимоги. Багато з них – для блага своїх студентів, звичайно – не вагаються детально визначити правила, за якими мають розв’язуватися задачі.
Один з користувачів мого Курсу невизначених інтегралів написав мені в GG таке:
у мене прохання, чи не могли б Ви на своєму FB або блозі показати, як інтеграли у Ваших формулах доводяться до вигляду на аркуші? Маю на увазі формули №: 5, 9, 10, 13, 14, 15, 16. На жаль, у нас пані професор сказала, що можна використовувати лише найпростіші, а ті, що я вказав, потрібно самому розбити до заданого вигляду. Думаю, багато людей були б Вам вдячні 🙂
Йдеться про аркуш з формулами, доданий до Курсу:
Формули для невизначених інтегралів
А конкретно про формули:
5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}
10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C
13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}
14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-а}{x+а} \right|+C}
15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}
16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}
Якщо не ці, то інші
Так, це правда, професори часто вимагають використовувати певні формули, а не інші. Або не використовувати деякі взагалі. Або використовувати ті, які нам не подобається використовувати.
Єдиний розумний вихід у таких ситуаціях, звичайно, це повна покора. В екзаменаційній залі викладач – це закон, і немає сенсу скаржитися пізніше друзям, що професор не прийняв колоквіум, хоча “мав би”.
Замість цього я перегляну зазначені формули одну за одною і покажу, як справлятися з кожним випадком окремо (на жаль, їх не можна “охопити” якимось спільним правилом). “Справлятися” означає розв’язувати інтеграли, що вимагають використання цієї формули без її використання – але з використанням менш загальної формули або виведенням інтегралу через підстановку чи раціональний метод.
Отже, по черзі:
5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}
З цією формулою, власне, не знаю, в чому проблема, вона ж випливає прямо з обернення формули похідної:
{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln aТож тут я не виявляю повної покори професору, а прошу пояснення, як мені, будь ласка, порахувати \int{{{3}^{x}}dx} не використовуючи формулу \int{{{a}^{x}}dx}.
Якщо хтось має цікаву ідею, благаю поділитися нею з людством у коментарях під постом.
9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}
Добре, повертаємося до гри.
Ця формула не випливає безпосередньо з обернення якоїсь формули похідної.
Якщо ми домовляємося, що не знаємо її, інтеграл \int{tgxdx} можемо порахувати через підстановку:
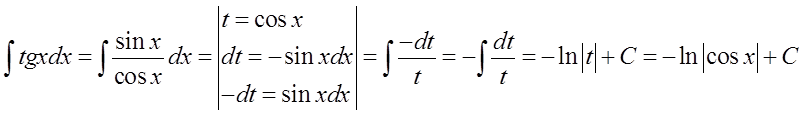
Тут аналогічно до попередньої:
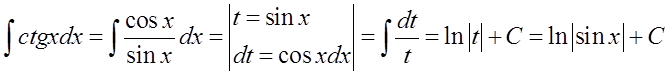
Ця формула є загальною формою формули:
\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} або: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}
Професор має на увазі, що ми повинні використовувати формулу: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} (що випливає з простої обернення формули похідної), а не використовувати формулу: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C} (яка вже є “обробленою” формулою).
Робимо це наступним чином (через перетворення і підстановку):
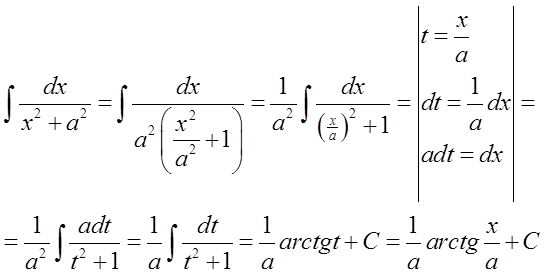
На конкретному прикладі це могло б виглядати так:
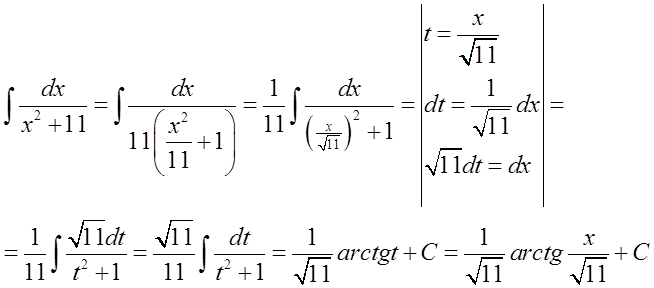
Ця формула відрізняється від попередньої, тут не йдеться про використання якоїсь формули, де замість ‘а’ є ‘1’ (такої формули немає). Альтернативою до використання цієї формули є тут проведення розкладу на прості дроби, як у раціональних інтегралах (я показав, як це робиться на Уроці 5 Курсу невизначених інтегралів).
Насправді, \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-а \right)\left( x+a \right)} і далі можна розкладати на прості дроби. Наприклад:
\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}Далі множимо на \left( x-3 \right)\left( x+3 \right), рахуємо сталі A, B порівнюючи поліноми і все так, як показано на Уроці 5 Курсу.
15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}Тут знову формула в загальному вигляді: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C} потрібно довести до формули в конкретному вигляді: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}.
Робимо це подібно до формули 13):
На конкретному прикладі це могло б виглядати так:
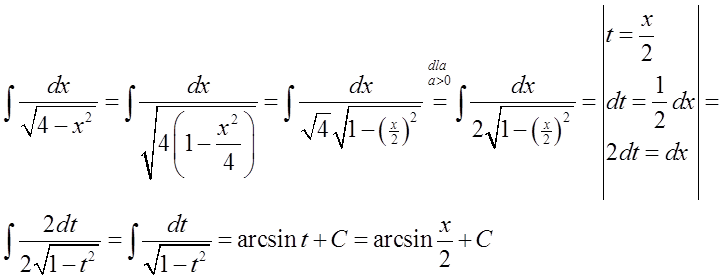
Справа складніша, вимагає використання так званих “гіперболічних підстановок” (гіперболічного синуса і косинуса). У цьому пості я залишаю цю тему, незабаром обов’язково напишу про ці підстановки.
Це всі формули, про які питав користувач, додам від себе, що додані мною до переліку основних формул:
\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+CВиводяться через просту підстановку: t=ax
Отже, маючи, наприклад, інтеграл: \int{{{e}^{-x}}dx} і НЕ маючи можливості скористатися (через вподобання професора) формулою \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C, використовуємо підстановку t=-x і спокійно рахуємо далі.