Підстановки Ейлера I роду (для a>0) – повторення
У попередньому пості:
ми розглядали інтеграли типу:
 ,
,
де a>0.
Ми також розв’язали приклад інтегралу, який відповідає цій умові, тобто
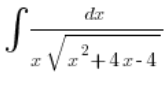
Але що, якщо ![]() в тричлені буде від’ємним (випадок, коли a=0 можна пропустити, бо тоді це не буде квадратний тричлен і інтеграл розв’язується через простіше підстановку
в тричлені буде від’ємним (випадок, коли a=0 можна пропустити, бо тоді це не буде квадратний тричлен і інтеграл розв’язується через простіше підстановку ![]() ніж підстановку Ейлера)?
ніж підстановку Ейлера)?
Тоді нам може допомогти (але не обов’язково…) другий тип підстановок Ейлера:
Підстановка Ейлера II роду (для c>0)
Маючи інтеграл типу:
 ,
,
де c>0, ми застосовуємо підстановку типу:
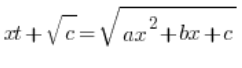 ,
,
яку знову підносимо обидві сторони до квадрату, де цього разу члени з ![]() скорочуються і які потрібно ще поділити обидві сторони на
скорочуються і які потрібно ще поділити обидві сторони на ![]() , щоб вийти на лінійну залежність, з якої визначимо за допомогою змінної
, щоб вийти на лінійну залежність, з якої визначимо за допомогою змінної ![]() в послідовності:
в послідовності:
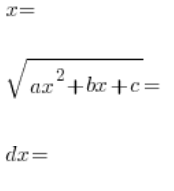
Підставляємо це все в інтеграл:

і знову виходимо на раціональний інтеграл, який – повторюю – зазвичай є трудомістким.
Почнемо з прикладу.
Приклад
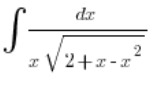
У квадратному тричлені дещо змінено порядок членів, але зрозуміло, що ![]() . Тобто
. Тобто ![]() не більше за
не більше за ![]() (тому ми не будемо застосовувати перший тип підстановок Ейлера), але c>0 (тобто застосуємо другий тип).
(тому ми не будемо застосовувати перший тип підстановок Ейлера), але c>0 (тобто застосуємо другий тип).
Підставляємо:
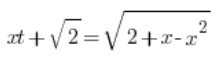
Підносимо обидві сторони до квадрату:
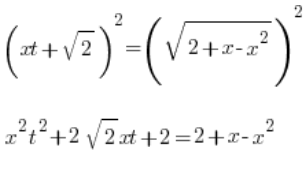
Член 2 скорочується (так має бути):
![]()
і тепер те, чого не було в першому типі підстановок, ділимо обидві сторони на x:
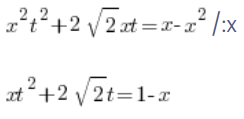
Далі визначаємо x:
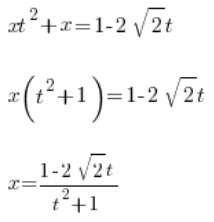
Маємо x визначене за допомогою змінної t. Тепер визначаємо 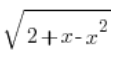 . Спочатку мали підстановку:
. Спочатку мали підстановку:
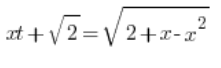
![]() вже визначене, тому просто підставляємо:
вже визначене, тому просто підставляємо:
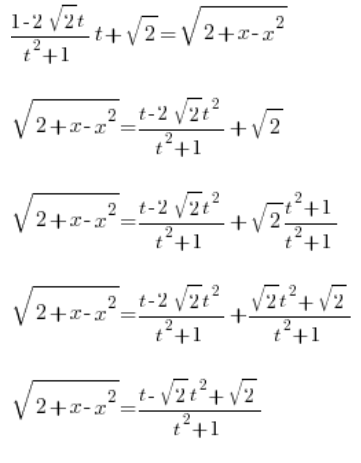
Залишається визначити тільки ![]() . Обчислимо це, взявши похідну від
. Обчислимо це, взявши похідну від ![]() :
:
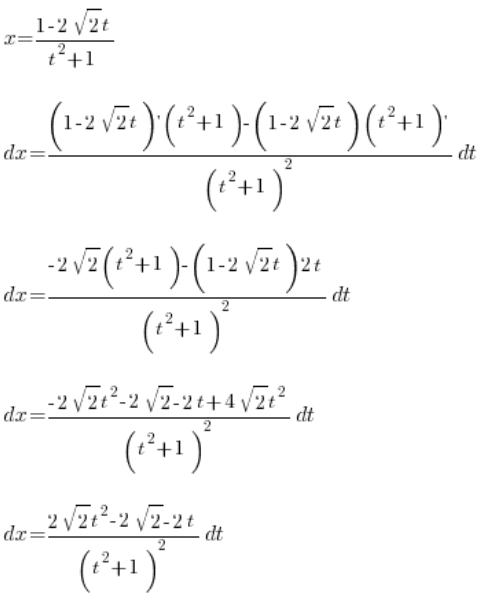
Маємо таке:
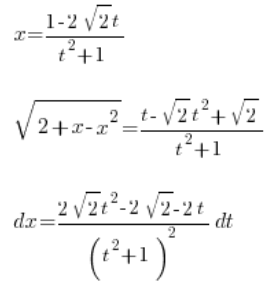
, все за допомогою змінної ![]() . Беремо інтеграл:
. Беремо інтеграл:
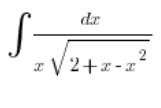
і підставляємо:
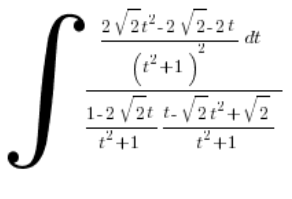
Беремось за очищення:
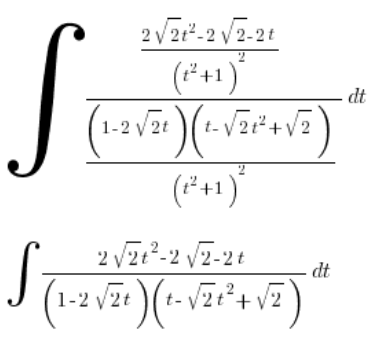
Повертаємось до підстановки:
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+CЩе треба повернутися з t до x. Нашою підстановкою Ейлера було
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}Звідки
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}Тобто наше рішення це
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+CЩо з іншими випадками?
Ми знаємо, що коли в інтегралі:

- a>0 – ми використовуємо перший тип підстановок
- c>0 – ми використовуємо другий тип підстановок
А що, якщо ні ![]() , ні
, ні ![]() не більші за нуль? Про це в наступному пості, де я розгляну третій тип підстановок Ейлера і покажу, що тема буде вичерпана, тобто для кожного типу інтегралів:
не більші за нуль? Про це в наступному пості, де я розгляну третій тип підстановок Ейлера і покажу, що тема буде вичерпана, тобто для кожного типу інтегралів:

…ми виберемо одну з трьох видів підстановок.


