Декілька речей, які ти повинен був добре вивчити в середній школі, але ніхто тобі цього не сказав – частина 2: квантори

---

Квантори – але цього взагалі не було…

Добре, я не на 100% впевнений, чи взагалі квантори залишилися у середній школі після регулярних щорічних скорочень матеріалу. Мені навіть не дуже хочеться це перевіряти, бо навіщо себе нервувати.

Вони повинні ще бути у розширеному профілі. Справді повинні.

Добре, але кому це потрібно?

У більшості математичних визначень і теорем використовуються поняття такі як: “кожен” і “існує”.

Найчастіше в якихось складніших послідовностях, наприклад, “між кожними двома числами є безліч чисел” (це трохи напівформально і неточно насправді), або: “для кожного невід’ємного дійсного числа існує рівно один його корінь”, або: “існує щось-там-щось-там, що для кожного іншого-щось-там існує ще інше-щось-там-щось-там” (це математичне визначення ще-іншого-щось-там).

У університеті ти отримаєш цілу купу таких визначень і теорем, продиктованих швидко і послідовно на лекції, або – що гірше – написаних одразу на дошці у вигляді:

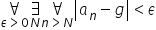
Було б добре (замість того, щоб піднімати руку і питати у Пана Професора, чи потрібно це “перемалювати”), щоб ти вже на початку вмів такі формули правильно читати. Ти міг би тоді відразу перейти до етапів “занурення” у визначення, кількох спостережень “як це працює” на конкретних прикладах тощо.

Загальний і специфічний квантор – познайомимося ближче

“кожен”, “для кожного” – це загальний квантор, позначається як: .

“існує”, “існує таке” – це специфічний квантор, позначається як: .

Я використовую і рекомендую саме такі знаки запису кванторів, бо вони точно не будуть плутатися один з одним.

– це перевернута велика літера A (від англійського “all” – кожен).

– це перевернута велика літера E (від англійського “exists” – існує).

Існують також інші позначення для кванторів: Λ (“для кожного”) і V (“існує”) – але ними займатися не буду, бо вони кожному плутаються.

Математичні формули, записані за допомогою кванторів

Найпростіші формули мають вигляд:

– читаємо: “для кожного x” (можна також записати: , але знову плутається, тому не буду цього робити)

– читаємо: “існує x”

Загалом, однак, формули є складнішими, наприклад:

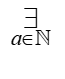– читаємо: “існує a, що є натуральним числом”, або: “існує таке a, яке належить до натуральних чисел”, або будь-який інший вираз українською мовою, що відображає суть справи, а саме:

1. Існує a

2. a є натуральним числом

Тут немає жодних “жорстких” мовних правил щодо того, яке має бути кожне слово і чи повинно бути “існує a”, чи повинно бути “існує таке a”.

Формули можна і найчастіше потрібно, поєднувати між собою, наприклад:

\underset{x>4}{\mathop{\forall }}\,\underset{n\in\mathbb{N}}{\mathop{\exists }}\,

означає:

“для кожного x>4 існує таке n, яке належить до натуральних чисел”

Ми розуміємо під цим, що для кожного x>4 “знайдемо” n, яке належить до натуральних чисел, щоб для кожного такого x вибрати відповідне n. Квантори залишаються між собою у логічному зв’язку, це не дві незалежні формули, записані поруч одна з одною.

Більше того…

Порядок має значення

Така сама формула, як остання, тільки зі зміненим порядком кванторів:

\underset{n\in \mathbb{N} }{\mathop{\exists }}\,\underset{x>4}{\mathop{\forall }}\,

…прочитаємо вже інакше:

“існує a, що є натуральним числом, що для x більше 4 …”

Ми розуміємо, що спочатку маємо якесь n (про яке знаємо, що воно існує) і тільки для цього встановленого n щось таке відбувається, що для всіх x>4 щось відбувається.

Приклад – відступ

Класичним прикладом є тут визначення рівномірної та точкової збіжності послідовності функцій, які відрізняються лише… порядком кванторів (трохи спростив ці визначення):

Точкова збіжність:

Рівномірна збіжність:

У визначенні рівномірної збіжності квантор, що був на початку точкової, опинився в кінці. Не заглиблюючись у подробиці, це змінює сенс всієї формули.

У точковій збіжності НАЙПЕРШЕ (читаємо зліва) брали якесь довільне x, потім, читаючи формулу, доходили до того, що для цього встановленого спочатку x відстані між значеннями функцій у послідовності та “граничною” функцією зменшуються до нескінченності.

У рівномірній збіжності НАЙПЕРШЕ стверджували, що відстань між значеннями відповідних функцій зменшується до нескінченності, а потім доходили до того, що таке відбувається для довільного x.

Запис визначень, теорем

Вміючи читати квантори, запис математичних визначень і теорем для нас вже відкритий. Наприклад:

\underset{x\in\mathbb{R}}{\mathоп{\forall }}\,{{x}^{2}}\ge 0

Прочитаємо як: “Для кожного дійсного числа x, x у квадраті більше або дорівнює нулю”, або якось гарніше: “Кожне число x, піднесене до квадрату, не від’ємне” – я однозначно за те, щоб читати визначення і теореми якоюсь більш барвистою мовою.

Речення вище є ПРАВДИВИМ. У нас немає жодних проблем писати також і ХИБНІ речення:

\underset{a>0}{\mathop{\exists }}\,\underset{x>a}{\mathop{\forall }}\,\frac{a}{x}>1

Або прочитали б: “Існує таке додатне число a, що для кожного числа x більше цього a, a поділене на x більше 1”, що є, звісно, ХИБОЮ (бо додатне число, поділене на більше за нього, ніколи не буде більше за 1, і немає такого числа).

А взявши зараз на розгляд визначення границі послідовності з попереднього посту:

Прочитаємо його так (додаючи трохи пояснень):

“Для довільного більшого за нуль знайдемо такий номер елемента послідовності , що для кожного елемента послідовності з номером більшим за відстань (модуль – це відстань) між цим елементом послідовності і межею буде меншою за ”

Можна також використати більш людську мову:

“Як би ми не встановили малу відстань на початку, знайдемо такий номер елемента послідовності, що всі наступні елементи цієї послідовності будуть ближче до межі , ніж встановлена на початку відстань “