Ранг матриці з параметром
Krystian Karczyński
Засновник та керівник сервісу eTrapez.
Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.
Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.
Візьмемо для обчислення ранг матриці:
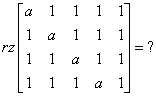
Розв’язання
Можна взятися за це кількома способами, і, мабуть, найшвидше буде помножити п’ятий стовпчик на -1 і додати до першого, другого, третього і четвертого, отримуючи таким чином:
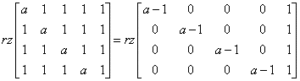Тепер візьмемо визначник матриці четвертого порядку:
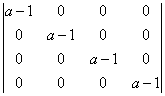Визначник, у якого всі елементи, крім головної діагоналі, дорівнюють нулю, дорівнює добутку елементів на головній діагоналі (колись я ще це доведу 🙂 ), отже:
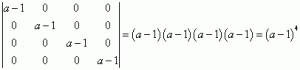Цей визначник не дорівнює нулю для всіх a, відмінних від 1. Отже, для таких a ранг нашої матриці, який ми маємо обчислити, дорівнює 4 (бо можна з неї виділити ненульовий мінор 4-го порядку, а більшого вже не можна).
А що з випадком, коли 
. Отримуємо тоді ранг матриці (підставляючи за a одиницю):
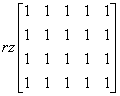І цей ранг дорівнює 1 (можна, наприклад, знову діючи п’ятим стовпчиком на інші та викресливши нульові стовпчики).
Отже, для a, відмінного від 1, ранг матриці дорівнює 4, а для a, рівного 1, ранг матриці дорівнює 1.
Шукаєте репетитора з математики для університетського рівня або школи? А може вам потрібен курс, який підготує вас до вступних іспитів?
Ми - команда eTrapez. Ми вчимо математику ясно, просто і дуже детально - дістанемося навіть до найбільш відсторонених від знань.
Ми створили курси відео зрозумілою мовою для завантаження на комп'ютер, планшет або телефон. Вмикайте запис, дивіться і слухайте, як на репетиторстві. У будь-який час дня та ночі.
