Візьмемо наступну межу послідовності:
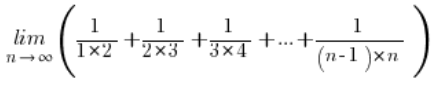
У задачі ми відчуваємо, що потрібно використовувати формули суми послідовності (арифметичної або геометричної), але, на жаль, ця послідовність не є ані арифметичною, ані геометричною…
Що робити?
Потрібно робити це зовсім інакше. Кожний дріб розкласти на прості дроби. Це робиться досить інтенсивно при розв’язанні невизначених інтегралів для раціональних функцій. Ідея полягає в тому, щоб знайти такі сталі A та B, щоб…
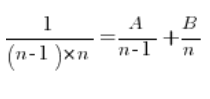
Множимо обидві сторони наведеного рівняння на 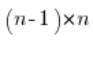 і отримуємо:
і отримуємо:
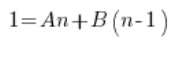
Далі:
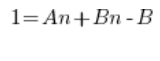
Порівнюємо коефіцієнти поліномів з лівої та правої сторін (рівність поліномів – середня школа) і отримуємо систему рівнянь:
![]() З другого рівняння:
З другого рівняння: ![]() .
.
Підставляючи це в перше рівняння:
![]()
Маємо також ![]() .
.
Отже, будь-який дріб можна розкласти на:
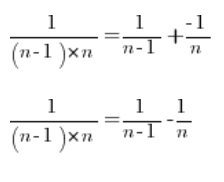
Повертаючись до нашої межі послідовності та розкладаючи кожен дріб на прості дроби:
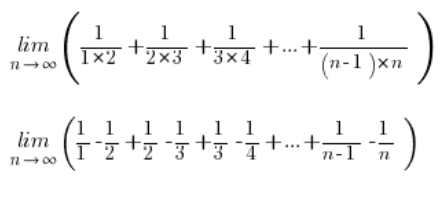
Скорочуючи частину складників, отримуємо:
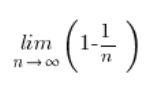
І ця межа послідовності вже не виглядає страшною, звичайно:
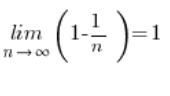
P.S.
Багато цікавих прикладів меж послідовностей можна знайти в моєму відео курсі, присвяченому межам.


