Цей пост присвячений фрагменту завдання на ЗНО, яке надіслав мені електронною поштою один випускник. Проте варто з цікавості подивитися і більше ніколи не казати, що математика в університеті важча, ніж розширена в школі.
🙂
Частина Завдання
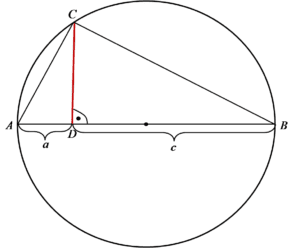
Маємо таку ситуацію:
Необхідно показати, що виділений червоним відрізок має довжину ![]() . Це, звичайно, лише маленький фрагмент усього завдання. Вгадайте, про що це? Про послідовності, звісно 🙂
. Це, звичайно, лише маленький фрагмент усього завдання. Вгадайте, про що це? Про послідовності, звісно 🙂
Отже, тут можна скористатися часто використовуваною в задачах на висоту прямокутного трикутника хитрістю, яка полягає в застосуванні подібних трикутників, улюблених усіма випускниками.
1. Трикутники ![]() (найменший) і
(найменший) і ![]() (найбільший, вписаний у коло) подібні (вони мають 2 однакові кути: прямий і <DAC, тобто третій кут також однаковий, отже, ми маємо подібність за двома кутами). Трикутники
(найбільший, вписаний у коло) подібні (вони мають 2 однакові кути: прямий і <DAC, тобто третій кут також однаковий, отже, ми маємо подібність за двома кутами). Трикутники ![]() (середній) і
(середній) і ![]() (найбільший знову) також подібні (вони мають 2 однакові кути: прямий і <CBD, тобто третій кут також однаковий, тобто ми знову маємо подібність за двома кутами). Якщо трикутники
(найбільший знову) також подібні (вони мають 2 однакові кути: прямий і <CBD, тобто третій кут також однаковий, тобто ми знову маємо подібність за двома кутами). Якщо трикутники ![]() і
і ![]() подібні до
подібні до ![]() , то вони також подібні один до одного, і ось що ми помічаємо:
, то вони також подібні один до одного, і ось що ми помічаємо:
![]() подібний до
подібний до ![]()
2. Якщо ці трикутники подібні, то співвідношення ВІДПОВІДНИХ сторін будуть рівні. Звичайно, ми вибираємо співвідношення, що містять червоний відрізок, довжину якого позначимо як ![]() .
.
У трикутнику ![]() співвідношення НАЙКОРОТШОЇ сторони до СЕРЕДНЬОЇ буде рівним:
співвідношення НАЙКОРОТШОЇ сторони до СЕРЕДНЬОЇ буде рівним:
![]()
У трикутнику ![]() співвідношення НАЙКОРОТШОЇ сторони до СЕРЕДНЬОЇ буде рівним:
співвідношення НАЙКОРОТШОЇ сторони до СЕРЕДНЬОЇ буде рівним:
![]()
Оскільки трикутники подібні, то існує рівність:
![]()
3. З цієї рівності визначаємо h, тобто довжину червоного відрізка. Перемножуємо хрест-навхрест, як це було в пропорціях, і отримуємо:
![]()
Тобто:
![]()
Тобто це те, що нам потрібно було показати на початку. БІНГО.
Висновок такий: при визначенні висоти в прямокутному трикутнику (той, що опускається на гіпотенузу звичайно), часто потрібно користуватися подібністю трикутників, як показано вище.
І ще один висновок: розширена математика в школі могла бути дійсно складною. Тільки в університеті ми можемо зітхнути з полегшенням 🙂