Немає товарів у кошику.
Krystian Karczyński- 28 Червня 2024
- Komentarz 0
Для відповіді на питання, поставлене в заголовку, нам не потрібно звертатися до визначення косої асимптоти, достатньо знати, що таке функція.
Як часто буває в математиці, уявимо собі, що графік функції МАЄ дві різні косі асимптоти при 
і покажемо, що, приймаючи це припущення, ми неодмінно дійдемо до суперечності, отже, це припущення не можна прийняти.
Графік
На графіку ці асимптоти могли б виглядати приблизно так:
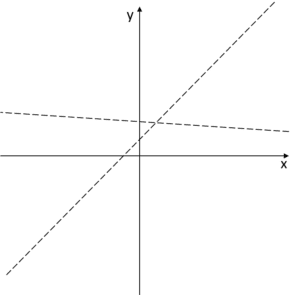І графік функції повинен наближатися до цих асимптот при , отже, виглядатиме наступним чином:
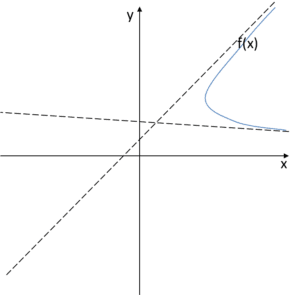І що? Може так бути? Чи може графік функції виглядати таким чином? Чи все ж у нас тут є проблема?
Проблема
Звичайно, у нас є проблема. Те, що показано вище, не може бути графіком функції. Звернімося до джерел, функція за визначенням – це відповідність, яка кожному аргументу x призначає точно одне значення y. Що випливає з нашого графіка?
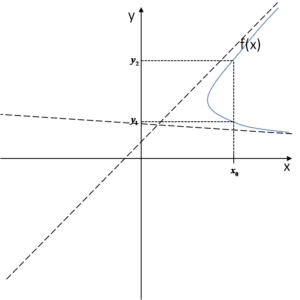З нього можна прочитати, що, наприклад, аргументу 
відповідають два значення – 
і 
. А це не може бути у графіку функції, оскільки кожному аргументу x має відповідати тільки одне значення y.
Отже, функція не може мати двох різних косих асимптот при . Все міркування можна повторити відповідно для 
🙂
