Currently Empty: zł0.00
Krystian Karczyński- 21 Червня 2024
- Comment 0
Визначення рангу матриці та його наслідки
Припустимо, ми визначили ранг матриці як: “кількість лінійно незалежних рядків і стовпців у матриці”. Які властивості рангу випливають з цього визначення відразу?
По-перше, очевидно, що ранг матриці може бути рівним: 1, або 4, або іноді 0. Але точно не буде рівним: -4, чи 
.
Добре, це все, що з нього випливає?
Але чи це все, що можна витиснути? Візьмемо, наприклад, матрицю:
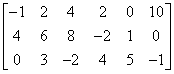
Ця матриця має 3 рядки і 6 стовпців.
Запитаймо себе, який може бути ранг цієї матриці? Чи може він бути рівним 7? Очевидно, що ні, тому що якщо ранг матриці – це “кількість лінійно незалежних рядків і стовпців”, то в цьому випадку він не може бути рівним 7, адже ця матриця не має стільки рядків або стовпців!
А тепер складніше запитання… Чи може ранг бути рівним 6? Адже у матриці є 6 стовпців…
Відповідь: ні. 6 має бути “кількістю лінійно незалежних рядків і стовпців”. 6 може бути кількістю лінійно незалежних стовпців (бо їх є 6), але не може бути кількістю лінійно незалежних рядків (бо їх тільки 3). А має бути кількістю лінійно незалежних “рядків і стовпців”.
Отже, очевидно, що ранг цієї матриці може бути максимально рівним 3.
Ми підходимо до корисної властивості:
ранг(A) <= min(кількість рядків у матриці, кількість стовпців у матриці)
Таким чином, дивлячись на матрицю, можна одразу сказати, яким є її максимальний ранг – що іноді буває дуже корисним.
Для більш точного обчислення потрібно використовувати відповідні методи – я показую їх у своєму Курсі по матрицях на Уроці 5, запрошую!
Related Posts
Порада Декарта – Не розумієш? ЗУПИНИСЯ!
Posted on
