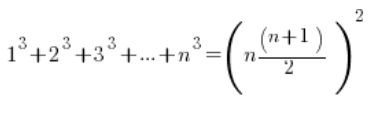Немає товарів у кошику.
Krystian Karczyński- 5 Серпня 2024
- Komentarz 0
У межах послідовностей іноді буває так:
а іноді навіть так:
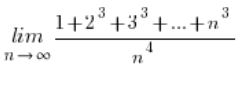
Що тоді?
Відповідь проста:
формули для суми квадратів та суми кубів послідовних натуральних чисел.
Вони йдуть так:
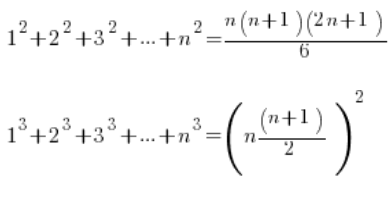
Формули – як і всі формули – треба вивчити напам’ять. Якщо у вас були схожі приклади і вони вам дійсно потрібні.
Знаючи ці формули, обчислення наших меж стає дуже простим:
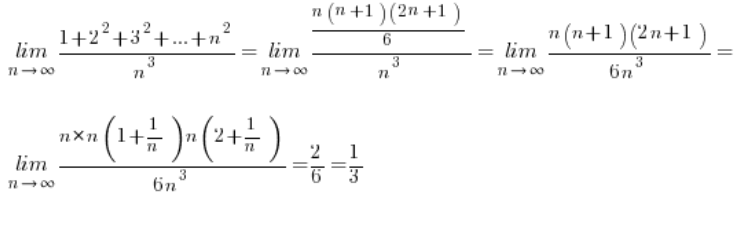
Наступна межа:
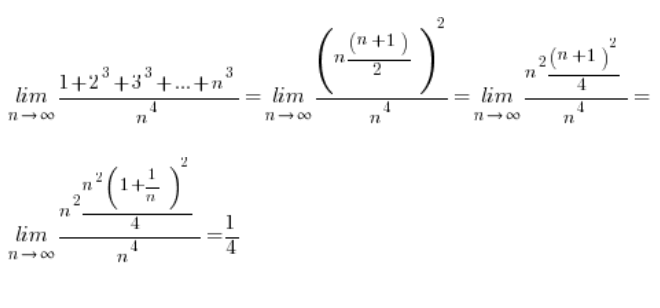
Індукційні докази для формул
Правильність формул можна досить легко довести індукцією (принаймні ще кілька років тому це був повний стандарт у школі). Я зроблю це для формули:
1. 
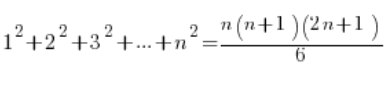
1 Крок індукції
Перевіряємо правильність формули для n=1:
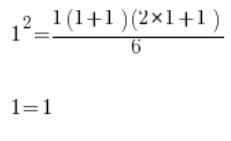
Все правильно
2 Крок індукції
Припускаємо гіпотезу, що для певного натурального n:
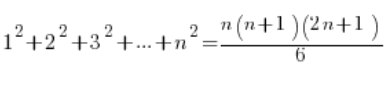
3 Крок індукції
Доводимо тезу (використовуючи прийняте припущення), що для n+1 формула також виконується, тобто:
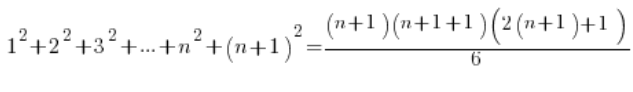
Зліва замість 
підставляємо формулу з гіпотези, справа просто упорядковуємо:
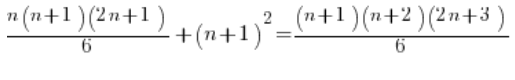
І далі, замість того, щоб силувати, працюємо трохи тонше:
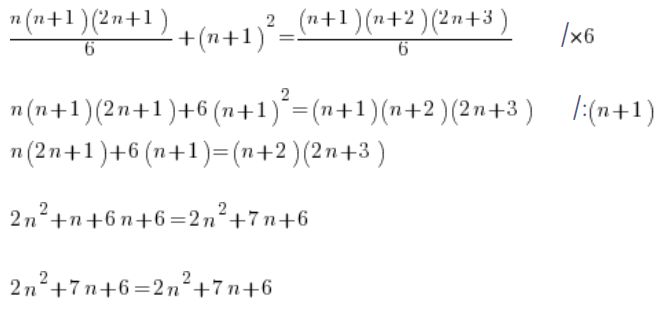
Тобто тезу доведено. Формулу доведено індукцією.
Запрошую вас довести індукцією другу формулу, для суми кубів:
