Немає товарів у кошику.
Krystian Karczyński- 24 Липня 2024
- Komentarz 0
При обчисленні квадратних коренів у декартовій (або: алгебраїчній) формі в моєму Курсі Комплексних Чисел я показав метод, що полягає в додаванні третього рівняння до вже існуючої системи з двох рівнянь, що в результаті значно спрощувало і скорочувало подальші обчислення.
Я показав цей метод, але ніяк його не обґрунтував.
І нещодавно я отримав листа з цього приводу:
Привіт
Чи могли б Ви пояснити, чому ми можемо використовувати метод додавання третього рівняння при обчисленні квадратного кореня з комплексного числа?
x^2 + y^2 = модуль числа, квадратний корінь якого ми обчислюємо
Це дуже гарне запитання і справді благословенні в математиці ті, хто не вірить професорам на слово, а завжди питають: “А звідки це взялося?” 🙂
Обґрунтування
Тож мені не залишається нічого іншого, як обґрунтувати цей метод одним із можливих способів:
Після перших кількох кроків у обчисленні квадратного кореня маємо таку ситуацію:
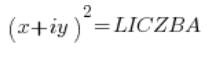
Оскільки числа (я не буду кожного разу писати: “комплексні числа”) зліва і справа рівні, то їх модулі також повинні бути рівні (зворотне не виконується, але це не важливо), тобто:
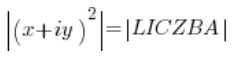
Число в квадраті – це число, помножене саме на себе, тобто:
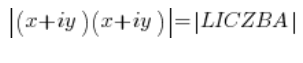
Модуль комплексного числа має властивість: 
, тобто зліва ми можемо записати:
… і при обчисленні модулів зліва ми маємо:
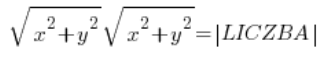
тобто:
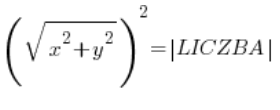
тобто:
тобто:
БІНГО
Дякую за гарне запитання!
