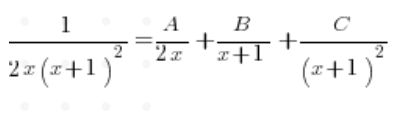Дельта дорівнює нулю у невизначених раціональних інтегралах

Розклад квадратичного тричлена на множники

У невизначених раціональних інтегралах часто є необхідність розкласти квадратичний тричлен на множники: 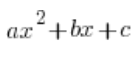. Ми це робимо зазвичай за допомогою формули: 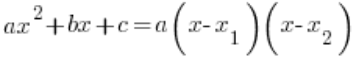, яка працює, коли .

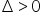Раціональні інтеграли і дельта дорівнює 0

Як виглядає цей двочлен, коли дельта дорівнює 0? Наприклад, як виглядає розклад на множники: ?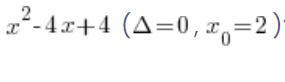

Чи може бути так:  ?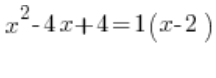

Звісно ні… Зі школи пам’ятаємо, що якщо , ми дійсно отримуємо один корінь, але це подвійний корінь. Тож у нашому прикладі можемо сказати: , що означає, що квадратичний тричлен, розкладений на множники, виглядає так:

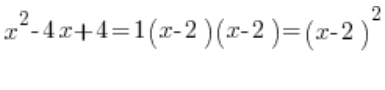
Це має значні наслідки у невизначених раціональних інтегралах, коли вони розкладаються на прості дроби.

Приклад

Візьмемо приклад:

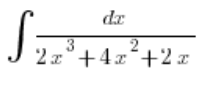
Розбираємо дріб без інтеграла, тобто пишемо:

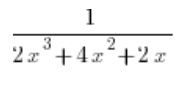
У знаменнику виносимо x перед дужкою:

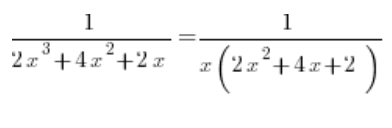
З квадратичного тричлена в знаменнику рахуємо дельту, вона дорівнює 0, і отримуємо корінь – (-1). Розкладаючи на множники, отримуємо:

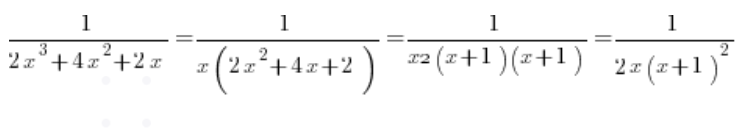
А розкладаючи на прості дроби: