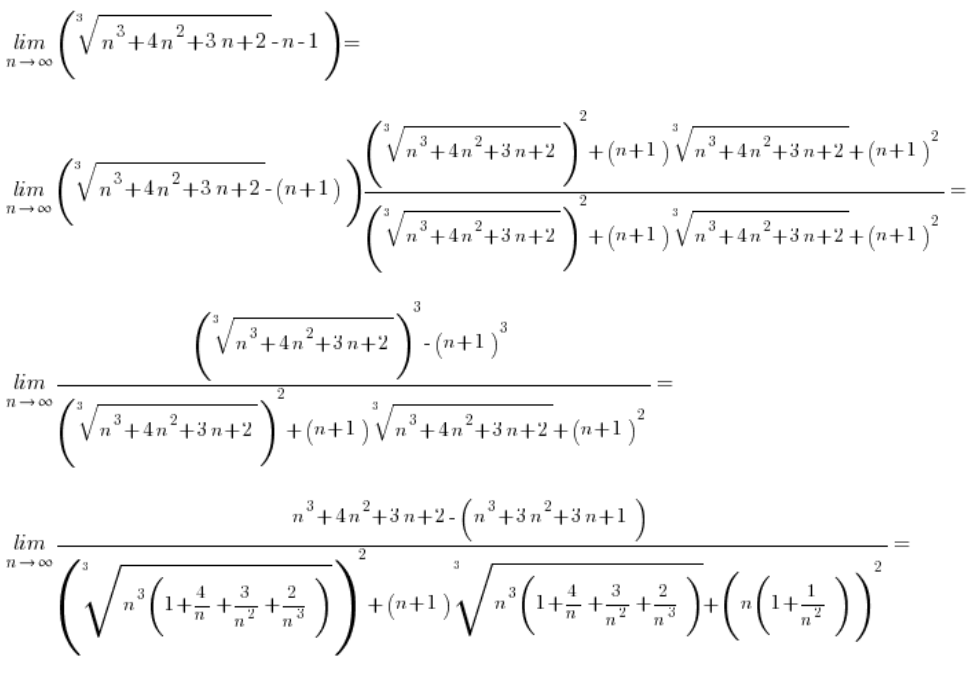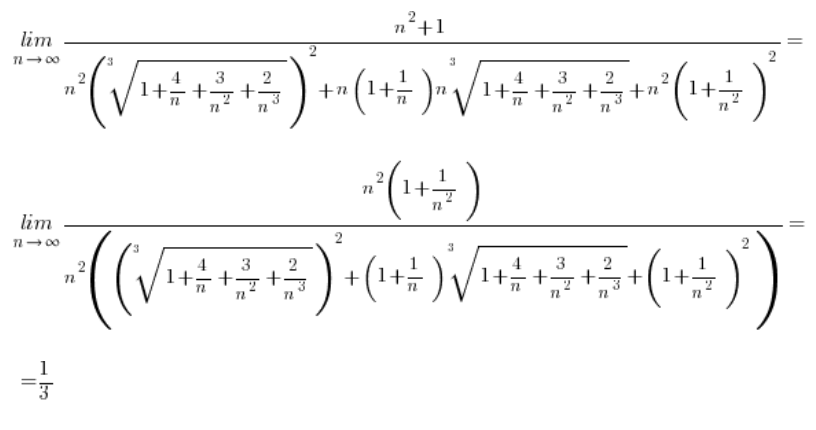Границя з кубічними коренями (Чи це множення на спряження?)
Krystian Karczyński
Засновник та керівник сервісу eTrapez.
Магістр математики Познанської Політехніки (Польща). Репетитор з математики з багаторічним досвідом. Творець перших Курсів eTrapez, які здобули величезну популярність серед студентів у всій Польщі.
Живе у Щецині (Польща). Любить прогулянки лісом, відпочинок на пляжі та каякінг.
Як це виглядало з “звичайними” коренями?
Коли ми мали обчислити границю, яка включала якесь віднімання з коренем (і яку, звісно, не можна було обчислити простіше), тобто:
“ЩОСЬ – корінь з чогось”
“корінь з чогось – ЩОСЬ”
“корінь з чогось – корінь з чогось”
ми використовували трюк, який я називаю – “множення на спряження”.
Ми просто множили цей вираз на його аналог зі знаком плюс, або точніше на дріб, де цей аналог був у чисельнику і знаменнику.
Наприклад:
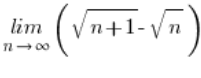ми множили так: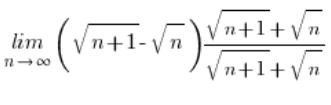 
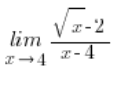ми множили так: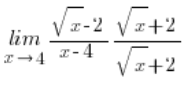 
Цей хитрий трюк дозволяв нам вийти на формулу скороченого множення:
Після виходу на цю формулу квадрати “скасовували” корені, і ми отримували простий результат (ну, іноді трохи довший простий результат).
Але що робити, коли корені, залучені у віднімання, будуть третього ступеня? Як, наприклад, тут:
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}Стандартний метод дій, тобто множення таким чином:
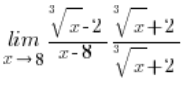
Нам нічого не дасть, тому що цього разу у чисельнику після виходу на формулу:
Квадрати жодним чином не “скорочують” корені третього ступеня. Тобто ми все ще будемо в глухому куті.
Як це виглядатиме з коренями третього ступеня?
У випадку віднімання з коренями третього ступеня потрібно просто “цілитись” у зовсім іншу формулу (але також із гімназії), а саме:
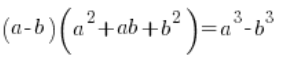
Тобто наші дані 
(де a або b або обидва – корені третього ступеня) замість множення на 
будемо множити на 
і після застосування формули куби зроблять свою роботу, “скорочуючи” корені.
Приклад 1
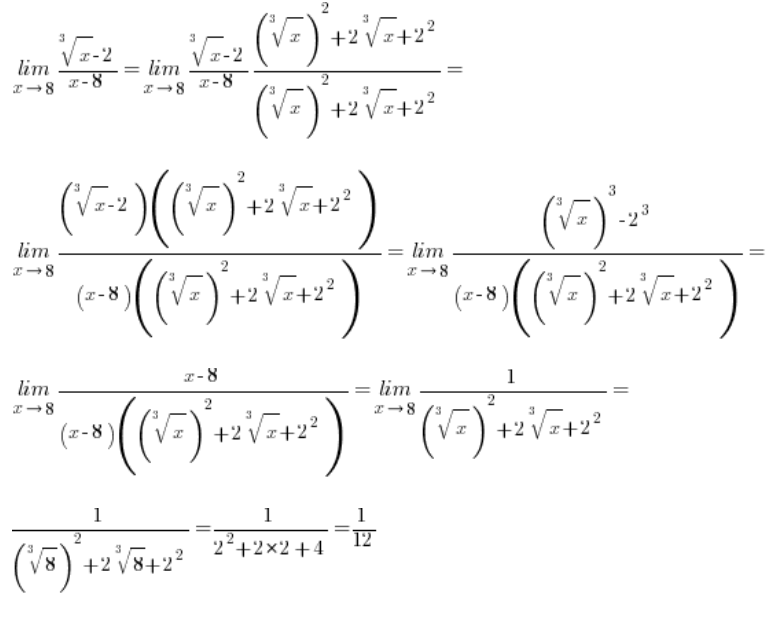
Приклад 2
Шукаєте репетитора з математики для університетського рівня або школи? А може вам потрібен курс, який підготує вас до вступних іспитів?
Ми - команда eTrapez. Ми вчимо математику ясно, просто і дуже детально - дістанемося навіть до найбільш відсторонених від знань.
Ми створили курси відео зрозумілою мовою для завантаження на комп'ютер, планшет або телефон. Вмикайте запис, дивіться і слухайте, як на репетиторстві. У будь-який час дня та ночі.
