Ekstrema Funkcji Wykład 6
Temat: Twierdzenie Fermata. Warunek konieczny istnienia ekstremum funkcji.
Streszczenie
Do badania zachowania się funkcji ![]() często wykorzystuje się jej pochodną
często wykorzystuje się jej pochodną ![]() . Na wykładzie przedstawię i udowodnię twierdzenie Fermata, które określa konieczny warunek istnienia ekstremum funkcji w punkcie odwołując się do jej pochodnej. Pokażę także, że nie jest to warunek wystarczający – na przykładzie punktów z funkcji, w których jest on spełniony, a jednak ekstremów w nich nie ma…
. Na wykładzie przedstawię i udowodnię twierdzenie Fermata, które określa konieczny warunek istnienia ekstremum funkcji w punkcie odwołując się do jej pochodnej. Pokażę także, że nie jest to warunek wystarczający – na przykładzie punktów z funkcji, w których jest on spełniony, a jednak ekstremów w nich nie ma…

Innymi słowy: jeżeli funkcja ma ekstremum w punkcie i ma pochodną w tym punkcie to na pewno, na pewno, na pewno pochodna z funkcji w tym punkcie równa jest zero.
Zwróćmy od razu uwagę (wrócimy do sprawy później), że twierdzenie Fermata nie zachodzi jakby „w drugą stronę”, to znaczy, z tego, że pochodna z funkcji w punkcie równa jest zero nie wynika, że w tym punkcie funkcja osiąga ekstremum.
Czyli jeszcze raz (upraszczając): jeśli mamy ekstremum, to mamy pochodną równą zero.
Aby dowieść Twierdzenie Fermata wprowadzę i udowodnię wcześniej lemat (o monotoniczności funkcji w zależności od jej pochodnej), który przydaje się nie tylko do tego dowodu:

Lemat ogólnie wyraża znaną i stosowaną zależność między zachowaniem się funkcji i jej pochodnej w punkcie.
Na przykład weźmy funkcję ![]() i jej pochodną
i jej pochodną ![]() . Narysujmy ich wykresy jeden pod drugim:
. Narysujmy ich wykresy jeden pod drugim:
 Widać, że funkcja
Widać, że funkcja ![]() jest rosnąca/malejąca w tych samych przedziałach, co jej pochodna
jest rosnąca/malejąca w tych samych przedziałach, co jej pochodna ![]() przyjmuje wartości większe/mniejsze od zera.
przyjmuje wartości większe/mniejsze od zera.
Lemat jest także doskonale „wyczuwalny” intuicyjne: skoro pochodna w punkcie wyraża przyrost wartości dla nieskończenie małego przyrostu argumentów, to jeśli wartość pochodnej będzie dodatnia, to przyrost tych wartości musi być też dodatni (funkcja musi „wzrosnąć”) i na odwrót – funkcja jest rosnąca.
Jeśli pochodna będzie ujemna, wartości musiały „zmaleć” – funkcja będzie malejąca.
Zabierzemy się teraz za ścisły dowód lematu. Aby to zrobić, musimy przypomnieć sobie (ze szkoły średniej) z definicji, co to znaczy, że funkcja „jest rosnąca” w punkcie i co to znaczy, że funkcja „jest malejąca” w punkcie.

Przyjrzyjmy się, jak „działa” te definicja funkcji rosnącej w punkcie na wykresie:
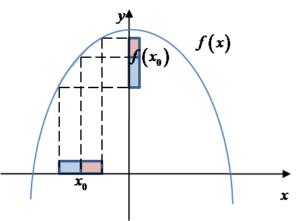 Na wykresie widać, że funkcja jest rosnąca w punkcie
Na wykresie widać, że funkcja jest rosnąca w punkcie ![]() . Jest rosnąca, ponieważ istnieje otoczenie prawostronne punktu
. Jest rosnąca, ponieważ istnieje otoczenie prawostronne punktu ![]() (na wykresie zaznaczono na czerwono na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie
(na wykresie zaznaczono na czerwono na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie ![]() (czyli f\left( {{x}_{0}} \right)>f\left( x \right)), a także ponieważ istnieje otoczenie lewostronne punktu
(czyli f\left( {{x}_{0}} \right)>f\left( x \right)), a także ponieważ istnieje otoczenie lewostronne punktu ![]() (na wykresie zaznaczono na niebiesko na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na niebiesko na osi OY) są mniejsze od wartości funkcji w punkcie
(na wykresie zaznaczono na niebiesko na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na niebiesko na osi OY) są mniejsze od wartości funkcji w punkcie ![]() (czyli
(czyli ![]() ).
).
Wiedząc już, co to konkretnie znaczy „rosnąca w punkcie” i „malejąca w punkcie” możemy się zabierać za dowód lematu:
  |
Mając udowodniony lemat o monotoniczności funkcji dowód Twierdzenia Fermata staje się dziecinnie prosty:
|
|
Twierdzenie Fermata jako warunek konieczny, ale nie wystarczający istnienia ekstremum funkcji w punkcie
Należy jeszcze raz podkreślić, że warunek konieczny istnienia ekstremum działa tak:
JEŻELI: Funkcja ma ekstremum w punkcie ![]() i pochodną w punkcie
i pochodną w punkcie ![]()
WTEDY: Pochodna funkcji w punkcie ![]() równa jest 0
równa jest 0
Nie działa on jednak tak:
JEŻELI: Pochodna funkcji w punkcie ![]() równa jest 0
równa jest 0
WTEDY: Funkcja ma ekstremum w punkcie ![]()
To ważne. W praktyce oznacza to, że aby pokazać, że funkcja osiąga ekstremum w punkcie nie wystarczy sprawdzić, czy jej pochodna w tym punkcie równa jest zero.
Przykład
Weźmy funkcję ![]() . Jej pochodna równa jest
. Jej pochodna równa jest ![]() . Jej pochodna w punkcie
. Jej pochodna w punkcie ![]() jest jak najbardziej równa 0 (bo
jest jak najbardziej równa 0 (bo ![]() ), ale ekstremum, jak widzimy na wykresie tej funkcji ni ma…
), ale ekstremum, jak widzimy na wykresie tej funkcji ni ma…
 Możliwe są różne inne akcje, na przykład funkcja
Możliwe są różne inne akcje, na przykład funkcja ![]() w punkcie
w punkcie ![]() w ogóle nie posiada pochodnej (pokazywałem na Wykładach z pochodnych) – a ekstremum ma jak najbardziej (można narysować i zobaczyć).
w ogóle nie posiada pochodnej (pokazywałem na Wykładach z pochodnych) – a ekstremum ma jak najbardziej (można narysować i zobaczyć).
Widzimy więc, że samo Twierdzenie Fermata nie wystarczy nam do tego, aby ekstrema funkcji wyznaczać…
KONIEC
Pisząc tego posta korzystałem z…
1. „Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.
Kliknij tutaj, aby przypomnieć sobie, czym są ekstrema funkcji (poprzedni Wykład) <–
Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji


Aga
Wszędzie jest napisane Lemat zamiast Temat.Pozdrawiam 🙂
Ola
Lemat to twierdzenie pomocnicze. W tym wypadku błędu nie ma. Pozdrawiam 😉
Piotr
Tak jest, gdy dzieciaki próbują nauczać MATEMATYKI WYŻSZEJ 🙂
Bartosz
Każdemu zdarza się drobny błąd. Akurat ten blog jest bardzo przydatny dla studentów i jeden mały błąd na tyle wykładów to coś normalnego. Profesorowie na mojej uczelni, którzy wykładają matematykę bardzo często robią błędy. Studenci myślący wyłapią te błędy i poprawią. A ten błąd to błąd klasyczny 😀 pozdrawiam
Jakub Pytlik
(zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie x0 (czylif(x0)>f(x))—-> czy nie powinno być na odwrót?, bo z rysunku co innego wynika. Pozdrawiam
Andrzej
W definicji funkcji rosnącej i malejącej jest chyba drobny błąd