fbpx

Twierdzenie Fermata. Warunek konieczny istnienia ekstremum.

 

Ekstrema Funkcji Wykład 6

 

Temat: Twierdzenie Fermata. Warunek konieczny istnienia ekstremum funkcji.

 

Streszczenie

Do badania zachowania się funkcji f(x) często wykorzystuje się jej pochodną f{prime}(x). Na wykładzie przedstawię i udowodnię twierdzenie Fermata, które określa konieczny warunek istnienia ekstremum funkcji w punkcie odwołując się do jej pochodnej. Pokażę także, że nie jest to warunek wystarczający – na przykładzie punktów z funkcji, w których jest on spełniony, a jednak ekstremów w nich nie ma…

Twierdzenie Fermata (warunek konieczny istnienia ekstremum funkcji w punkcie)

Niech funkcja f(x) określona w pewnym przedziale delim{[}{a,b}{]} osiąga w punkcie wewnętrznym x_0 tego przedziału ekstremum (maksimum lub minimum). Jeśli istnieje w tym punkcie pochodna skończona f{prime}(x_0), to na pewno:

f{prime}(x_0)=0

Innymi słowy: jeżeli funkcja ma ekstremum w punkcie i ma pochodną w tym punkcie to na pewno, na pewno, na pewno pochodna z funkcji w tym punkcie równa jest zero.

Zwróćmy od razu uwagę (wrócimy do sprawy później), że twierdzenie Fermata nie zachodzi jakby “w drugą stronę”, to znaczy, z tego, że pochodna z funkcji w punkcie równa jest zero nie wynika, że w tym punkcie funkcja osiąga ekstremum.

Czyli jeszcze raz (upraszczając): jeśli mamy ekstremum, to mamy pochodną równą zero.

Aby dowieść Twierdzenie Fermata wprowadzę i udowodnię wcześniej lemat (o monotoniczności funkcji w zależności od jej pochodnej), który przydaje się nie tylko do tego dowodu:

Lemat o monotoniczności funkcji

Niech funkcja f(x) ma w punkcie x_0 pochodną skończoną:

Jeśli pochodna w tym punkcie przyjmuje wartość dodatnią, to funkcja f(x) jest w tym punkcie rosnąca.

Jeśli pochodna w tym punkcie przyjmuje wartość ujemną, to funkcja f(x) jest w tym punkcie malejąca.

Lemat ogólnie wyraża znaną i stosowaną zależność między zachowaniem się funkcji i jej pochodnej w punkcie.

Na przykład weźmy funkcję f(x)=x^2 i jej pochodną f{prime}(x)=2x. Narysujmy ich wykresy jeden pod drugim:

Wykresy funkcji f(x)=x^2 i jej pochodnej f(x)=2xWidać, że funkcja f(x)=x^2 jest rosnąca/malejąca w tych samych przedziałach, co jej pochodna f{prime}(x)=2x przyjmuje wartości większe/mniejsze od zera.

Lemat jest także doskonale “wyczuwalny” intuicyjne: skoro pochodna w punkcie wyraża przyrost wartości dla nieskończenie małego przyrostu argumentów, to jeśli wartość pochodnej będzie dodatnia, to przyrost tych wartości musi być też dodatni (funkcja musi “wzrosnąć”) i na odwrót – funkcja jest rosnąca.

Jeśli pochodna będzie ujemna, wartości musiały “zmaleć” – funkcja będzie malejąca.

Zabierzemy się teraz za ścisły dowód lematu. Aby to zrobić, musimy przypomnieć sobie (ze szkoły średniej) z definicji, co to znaczy, że funkcja “jest rosnąca” w punkcie i co to znaczy, że funkcja “jest malejąca” w punkcie.

Definicja funkcji rosnącej w punkcieFunkcję f(x) nazywamy rosnącą w punkcie x_0, jeżeli istnieje takie prawostronne otoczenie punktu x_0, w którym dla każdego x z tego otoczenia: f\left( {{x}_{0}} \right)>f\left( x \right) i istnieje takie lewostronne otoczenie punktu x_0, w którym dla każdego x z tego otoczenia: f(x)<f(x_0).
Definicja funkcji malejącej w punkcieFunkcję f(x) nazywamy malejącą w punkcie x_0, jeżeli istnieje takie prawostronne otoczenie punktu x_0, w którym dla każdego x z tego otoczenia: f(x)<f(x_0) i istnieje takie lewostronne otoczenie punktu x_0, w którym dla każdego x z tego otoczenia: f\left( {{x}_{0}} \right)>f\left( x \right).

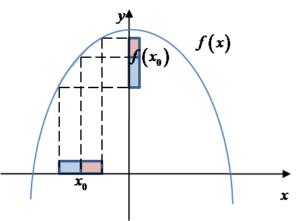
Przyjrzyjmy się, jak “działa” te definicja funkcji rosnącej w punkcie na wykresie:

Funkcja rosnąca w punkcie x_0Na wykresie widać, że funkcja jest rosnąca w punkcie x_0. Jest rosnąca, ponieważ istnieje otoczenie prawostronne punktu x_0 (na wykresie zaznaczono na czerwono na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie x_0 (czyli f\left( {{x}_{0}} \right)>f\left( x \right)), a także ponieważ istnieje otoczenie lewostronne punktu x_0 (na wykresie zaznaczono na niebiesko na osi OX) i dla x-sów z tego otoczenia odpowiadające im wartości (zaznaczone na niebiesko na osi OY) są mniejsze od wartości funkcji w punkcie x_0 (czyli f(x)<f(x_0)).

Wiedząc już, co to konkretnie znaczy “rosnąca w punkcie” i “malejąca w punkcie” możemy się zabierać za dowód lematu:

Dowód lematu o monotoniczności funkcji
Dowód lematu jest prosty i opiera się wprost na definicji pochodnej funkcji w punkcie.Jeżeli z założenia pochodna funkcji w punkcie x_0 jest większa od zera ( {f}'\left( {{x}_{0}} \right)>0) i z definicji pochodna ta jest równa (wcześniejsze Wykład): f{prime}(x_0)={lim}under{{Delta}x{right}0}{f(x_0+{Delta}x)-f(x_0)}/{{Delta}x} oznacza to, że z założenia: \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)}{\Delta x}>0 Skoro zachodzi ta nierówność, oznacza to, że dla pewnych, dostatecznie małych {Delta}x zachodzi: \underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)}{\Delta x}>0 Jeżeli założymy sobie do tego, że {Delta}x jest dodatnie (dąży do zera, ale jest dodatnie) i pomnożymy obie strony przez {Delta}x otrzymamy: f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)>0Czyli:f(x_0)<f(x_0+{Delta}x)A więc pokazałem, że dla pewnego prawostronnego sąsiedztwa x_0 (bo {Delta}x było dodatnie, zatem x_0 zwiększyłem) wartości funkcji w punkcie x_0 są mniejsze od wartości funkcji dla x-sów z tego prawostronnego sąsiedztwa punkto x_0.

 

Jeżeli zaś, założymy, że przyrost argumentów {Delta}x jest ujemny (ale dążący do zera), po przemnożeniu nierówności:

\underset{\Delta x\to 0}{\mathop{\lim }}\,\frac{f\left( {{x}_{0}}+\Delta x \right)-f\left( {{x}_{0}} \right)}{\Delta x}>0

…przez wartość ujemną uzyskamy (zmiana znaku):

f(x_0+{Delta}x)-f(x_0)<0

czyli:

f\left( {{x}_{0}} \right)>f\left( {{x}_{0}}+\Delta x \right)

A więc pokazałem, że w dostatecznie małym lewostronnym sąsiedztwie x_0 (x_0 powiększone o ujemny przyrost {Delta}x – a więc pomniejszone jednym słowem) wartości funkcji w punkcie x_0 są większe od wartości funkcji w tym sąsiedztwie.

Wykazałem więc w ten sposób pierwszą część naszego lematu:

Lemat o monotoniczności funkcji
Niech funkcja f(x) ma w punkcie x_0 pochodną skończoną:

Jeśli pochodna w tym punkcie przyjmuje wartość dodatnią, to funkcja f(x) jest w tym punkcie rosnąca.

Jako że wykazane przeze mnie nierówności oznaczają nie mniej nie więcej, a to, że funkcja jest rosnąca w punkcie z definicji.

Dowód drugiej części przebiegał by zupełnie analogicznie.

KONIEC DOWODU LEMATU O MONOTONICZNOŚCI FUNKCJI

Mając udowodniony lemat o monotoniczności funkcji dowód Twierdzenia Fermata staje się dziecinnie prosty:

Dowód Twierdzenia Fermata

Jeżeli (zgodnie z założeniami twierdzenia) funkcja f(x) osiąga w pewnym punkcie x_0 ekstremum i posiada w nim pochodną, to:

1. Jeżeli wartość tej pochodnej jest dodatnia ( f\left( {{x}_{0}} \right)>0) to zgodnie z lematem o monotoniczności funkcji funkcja w tym punkcie jest rosnąca.

Jeśli funkcja w tym punkcie jest rosnąca, to nie może w tym punkcie osiągać ekstremum. Faktycznie – jeśli jej wartości są większe od wartości na lewo od x_0 i mniejsze od wartości na prawo od x_0 – to na pewno nie istnieje żadne otoczenie punktu x_0 w którym wartość funkcji w punkcie x_0 jest największa, albo najmniejsza – a tak zdefiniowaliśmy ekstrema funkcji na poprzednim wykładzie. Pisząc prościej: jeśli funkcja jest w punkcie rosnąca, to zawsze będzie od czegoś większa i od czegoś mniejsza, a zgodnie z definicją ekstremum powinna być zawsze większa (maksimum), albo zawsze mniejsza (minimum).

Wartość pochodnej w punkcie x_0 nie może być zatem dodatnia.

2. Jeżeli wartość tej pochodnej jest ujemna (f{prime}(x_0)<0) to zgodnie z lematem o monotoniczności funkcji funkcja w tym punkcie jest malejąca.

Jeśli funkcja w tym punkcie jest malejąca, to nie może w tym punkcie osiągać ekstremum. Faktycznie – jeśli jej wartości są mniejsze od wartości na lewo od x_0 i większe od wartości na prawo od x_0 – to na pewno nie istnieje żadne otoczenie punktu x_0 w którym wartość funkcji w punkcie x_0 jest największa, albo najmniejsza – a tak zdefiniowaliśmy ekstrema funkcji na poprzednim wykładzie. Pisząc prościej: jeśli funkcja jest w punkcie malejąca, to zawsze będzie od czegoś większa i od czegoś mniejsza, a zgodnie z definicją ekstremum powinna być zawsze większa (maksimum), albo zawsze mniejsza (minimum).

Wartość pochodnej w punkcie x_0 nie może być zatem ujemna.

3. Skoro wartość pochodnej funkcji w punkcie nie może być ani dodatnia (1.), ani ujemna (2.), to musi koniecznie być równa 0, co należało wykazać.

KONIEC DOWODU TWIERDZENIA FERMATA

Twierdzenie Fermata jako warunek konieczny, ale nie wystarczający istnienia ekstremum funkcji w punkcie

Należy jeszcze raz podkreślić, że warunek konieczny istnienia ekstremum działa tak:

JEŻELI: Funkcja ma ekstremum w punkcie x_0 i pochodną w punkcie x_0

WTEDY: Pochodna funkcji w punkcie x_0 równa jest 0

Nie działa on jednak tak:

JEŻELI: Pochodna funkcji w punkcie x_0 równa jest 0

WTEDY: Funkcja ma ekstremum w punkcie x_0

To ważne. W praktyce oznacza to, że aby pokazać, że funkcja osiąga ekstremum w punkcie nie wystarczy sprawdzić, czy jej pochodna w tym punkcie równa jest zero.

Przykład

Weźmy funkcję f(x)=x^3. Jej pochodna równa jest f{prime}(x)=3x^2. Jej pochodna w punkcie x_0=0 jest jak najbardziej równa 0 (bo f{prime}(0)=3*0^2=0), ale ekstremum, jak widzimy na wykresie tej funkcji ni ma…

Funkcja f(x)=x^3 - brak ekstremum w punkcie x_0=0Możliwe są różne inne akcje, na przykład funkcja f(x)=delim{|}{x}{|} w punkcie x_0 w ogóle nie posiada pochodnej (pokazywałem na Wykładach z pochodnych) – a ekstremum ma jak najbardziej (można narysować i zobaczyć).

Widzimy więc, że samo Twierdzenie Fermata nie wystarczy nam do tego, aby ekstrema funkcji wyznaczać…

KONIEC

Pisząc tego posta korzystałem z…

1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.

 

Kliknij tutaj, aby przypomnieć sobie, czym są ekstrema funkcji (poprzedni Wykład) <–

Kliknij tutaj, aby zobaczyć, jakie warunki są wystarczające do istnienia ekstremum funkcji w punkcie (następny Wykład) –>

Kliknij, aby powrócić na stronę z wykładami o badaniu przebiegu zmienności funkcji

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany. Wymagane pola są oznaczone *

Twój komentarz będzie dostępny publicznie na naszej stronie razem z powyższym podpisem. Komentarz możesz zmienić, lub usunąć w każdej chwili. Administratorem danych osobowych podanych w tym formularzu jest eTrapez Usługi Edukacyjne E-Learning Krystian Karczyński. Zasady przetwarzania danych oraz Twoje uprawnienia z tym związane opisane są w Polityce Prywatności.


  1. Aga pisze:
    26 stycznia 2018 o 13:02

    Wszędzie jest napisane Lemat zamiast Temat.Pozdrawiam 🙂

    Odpowiedz
    1. Ola pisze:
      17 lutego 2018 o 15:45

      Lemat to twierdzenie pomocnicze. W tym wypadku błędu nie ma. Pozdrawiam 😉  

  2. Piotr pisze:
    1 lutego 2016 o 19:09

    Tak jest, gdy dzieciaki próbują nauczać MATEMATYKI WYŻSZEJ 🙂

    Odpowiedz
    1. Bartosz pisze:
      4 lutego 2016 o 00:33

      Każdemu zdarza się drobny błąd. Akurat ten blog jest bardzo przydatny dla studentów i jeden mały błąd na tyle wykładów to coś normalnego. Profesorowie na mojej uczelni, którzy wykładają matematykę bardzo często robią błędy. Studenci myślący wyłapią te błędy i poprawią. A ten błąd to błąd klasyczny 😀 pozdrawiam

  3. Jakub Pytlik pisze:
    4 lutego 2014 o 11:59

    (zaznaczone na czerwono na osi OY) są większe od wartości funkcji w punkcie x0 (czylif(x0)>f(x))—-> czy nie powinno być na odwrót?, bo z rysunku co innego wynika. Pozdrawiam

    Odpowiedz
  4. Andrzej pisze:
    27 grudnia 2013 o 13:04

    W definicji funkcji rosnącej i malejącej jest chyba drobny błąd

    Odpowiedz