Różne wyniki, poprawne rozwiązanie, w zadaniach na całki nieoznaczone – możliwe?
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Sprawdzając wynik swoich obliczeń w całkach nieoznaczonych z odpowiedziami na zadania np. na końcu podręcznika często dojść można do frustrującego punktu, w którym nam po prostu “wychodzi inaczej” i nie możemy pojąc dlaczego.
Skąd się biorą różnice?
Warto być świadomym, że obie odpowiedzi mogą być poprawne, to znaczy nasza i z podręcznika. Po pierwsze te samo wyrażenie można zapisać w różny sposób, na przykład:
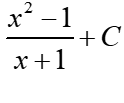
po skróceniu da nam:
A na przykład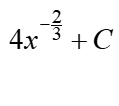 
to to samo co: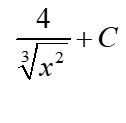 
Ciekawsze może być jednak to, że wyniki mogą się różnić o stałą i również nie ma z tym problemu, bo przecież sama całka nieoznaczona to z definicji rodzina funkcji różniących się o stałą.
Tak więc:
należy do tej samej rodziny funkcji, co:
bo różnią się tylko o stałą (-1). Oba wyniki są poprawne.
Do tej samej rodziny funkcji należała by też:
bo 
to stała tak samo jak 2 albo 3.
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Dziękuję za odpowiedź. Właśnie porównanie tych trzech różnych funkcji wzbudziło moją wątpliwość, ale pytanie jest praktycznie przepisaniem stwierdzenia z książki Romana Leitnera, Wojciecha Matuszewskiego i Zdzisława Rojka “Zadania z matematyki wyższej część II ” . Teraz już zrozumiałem całkowicie sens tych różnych wyników: po prostu te trzy funkcje trygonometryczne, np. dla kąta pi/4 zwrócą nam różne wartości, ale poprzez odpowiednie dobranie stałych ( dlatego oznaczono je jako C, C1 i C2 , żeby podkreślić, że wszystkie stałe nie muszą być takie same- zresztą z tego co widzę, to chyba nigdy te 3 stałe nie będą sobie równe jednocześnie) jesteśmy w stanie uzyskać tę samą wartość. Zanotowałem sobie to co Pan napisał: z równości pochodnych nie wynika równość funkcji ( podobnie jak kiedyś się zastanawiałem z panią doktor na studiach , czy z różniczkowalności funkcji ciągłej wynika ciągłość jej pochodnej, ale doszliśmy do wniosku, że NIE, bo np. skoro dystrybuanta jest całką z gęstości, więc pochodna dystrybuanty to gęstość- dystrybuanta jest zawsze ciągła( mówię tu o rozkładach ciągłych zmiennej losowej), ale jej pochodna, czyli gęstość zmiennej losowej, już ciągła wcale nie musi być 😉 ) . Autorzy zapisując równość pomiędzy tymi trzema różnymi funkcjami pewnie chcieli przez to powiedzieć, to co wyżej napisałem, ale jak widać, dla mnie np. sprawiło to problem, ale notabene widziałem w tej książce jeszcze kilka pomyłek ( może kiedyś powstanie kolejne wydanie z poprawkami 😉 ) A tak na sam koniec jak dla mnie ten problem jest dość ciekawy, chociaż można się było spodziewać, że dla tych trzech różnych funkcji można dobrać takie stałe, aby każda z jej wartości dla danego argumentu była taka sama ( w końcu są to funkcje okresowe, pochodzące od funkcji sinus(x) i cosinus(x) przesuniętych w fazie o pi/2 między sobą). Tak na pierwszy rzut oka to naprawdę ciężko jest wychwycić fakt, dlaczego te 3 różne funkcje są poprawnymi wynikami tej samej całki nieoznaczonej. Dziękuję raz jeszcze i pozdrawiam
Dzień dobry, chciałbym zadać pytanie odnośnie sytuacji, gdy wynik całkowania ma kilka postaci, np. całka z 2sinxcosx dx jest równa każdemu z wyrażeń:
sin^2(x) + C = – cos^2(x) + C1 = – 1/2 cos(2x) + C2 co łatwo sprawdzić przez różniczkowanie.
Ja zacząłem to udowadniać w taki sposób: sin^2(x) + 1/2 cos(2x)= sin^2(x) + 1/2(cos^2(x) – sin^2(x) )= 1/2(sin^2(x) + cos^2(x)) = 1/2
Czyli 1/2 = C1 – C , czyli C1 i C nie są DOWOLNYMI stałymi, tylko muszą być wymierne, a na dodatek dawać w różnicy (w sumie) 1/2
Podobnie jest w równaniu sin^2(x)+cos^2(x) = C1 – C tutaj też C1 i C nie są dowolnymi stałymi, ponieważ w różnicy (sumie) muszą dać 1.
I podobnie jest w równaniu – cos^2(x) + C1 = – 1/2 cos(2x)+ C2 , gdzie ostatecznie otrzymuję 1/2= C1-C2, czyli to też nie są dowolne stałe, bo muszą dać 1/2 . Bardzo proszę o pomoc w zrozumieniu tego, po zróżniczkowaniu rzeczywiście jest taki sam wynik, ale może źle rozumuję w moim “dowodzie” ?
Dzień dobry
Już wyjaśniam.
To, że całka z 2sinxcosx jest równa każdemu z wyrażeń: {{sin }^{2}}x+C,-{{cos }^{2}}x+{{C}_{1}},-\frac{1}{2}cos 2x+{{C}_{2}}, jest PRAWDĄ.
Natomiast to, że {{sin }^{2}}x+C=-{{cos }^{2}}x+{{C}_{1}}=-\frac{1}{2}cos 2x+{{C}_{2}}NIE JEST PRAWDĄ. Innymi słowy, te wyrażenia nie są wcale równe sobie. Te funkcje się RÓŻNIĄ o stałą.
Całka nieoznaczona jest to własnie rodzina funkcji różniących się (a nie równych sobie) o stałą.
Czyli z tego, że całka z 2sinxcosxdx równa się funkcji A oraz równa się funkcji B NIE wynika, że A = B.
To jest PRAWDA, jeżeli nałożymy warunek, że funkcje {{sin }^{2}}x+Ci -\frac{1}{2}cos 2x+{{C}_{2}}mają być równe, to rzeczywiście stałe Ci C_1nie mogą być zupełnie dowolne, ale te funkcje nie są i nie muszą być wcale równe 🙂
Prześledźmy to może jeszcze na prostszym przykładzie.
Funkcje f\left( x \right)=x+1i g\left( x \right)=x+2oczywiście nie są równe, bo: x+1\ne x+2.
Jednak ich pochodne: {f}'(x)=1i {g}’\left( x \right)=1są sobie równe, bo: 1=1.
Z równości pochodnych nie wynika równość funkcji.
Do całki (jako rodziny funkcji) z \int{1dx}należą zarówno funkcje f(x)=x+1, jak i g\left( x \right)=x+2– pomimo tego, że wcale nie są równe 🙂