Jeśli uczysz się matematyki na studiach już od jakiegoś czasu, z pewnością zauważyłeś, że większość materiału przerabianego w szkole średniej bezpośrednio w żaden sposób nie przydaje Ci się na studiach. Jeżeli dopiero zaczynasz naukę – zwróć na to uwagę.
Co znaczy „bezpośrednio”?
Zastrzegam się tylko, że napisałem „bezpośrednio”, bo oczywiście każda kropla Twojego matematycznego potu wyciśnięta w średniej nie zmarnuje się i zostanie Ci policzona. Chodzi mi o ćwiczenie się w abstrakcyjnym myśleniu, umiejętność koncentracji na problemie i takie tam różne.
Jednak – pisząc wprost – do mnóstwa z przerabianych w szkole średniej działów matematyki nie będziesz już musiał wracać, nawet po to, żeby sobie tam zajrzeć i coś powtórzyć.
Są jednak wyjątki.
Są rzeczy, przerabiane w szkole średniej, bez znajomości których na studiach daleko nie zajedziesz.
Na początku roku akademickiego warto je sobie powtórzyć, albo po prostu się ich nauczyć. Dzięki temu „utorujesz” sobie drogę do dalszych, nowych zagadnień. Nie przerobione – będą cały czas Ci uwierać, jak cierń w bucie, utrudniając (albo nawet uniemożliwiając) marsz do przodu.
Nie będą to całe wielki działy matematyki, tylko najczęściej drobne szczególiki, małe cegiełki, bez których cała budowla może się zawalić.
Definicja granicy
Weźmy na przykład definicję granicy ciągu, z którą zetkniesz się bardzo prędko:
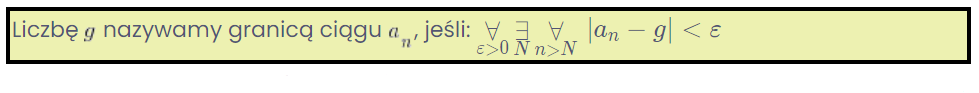
Rozumiesz z tych dziwnych znaczków po lewej? A z tej wartości bezwzględnej po prawej? Nie za wiele?
A przecież do zrozumienia, albo chociaż prawidłowego odczytania tej definicji powinna wystarczyć znajomość kwantyfikatorów (to te stwory po lewej: ![]() ) i interpretacji geometrycznej wartości bezwzględnej (po prawej) ze szkoły średniej…
) i interpretacji geometrycznej wartości bezwzględnej (po prawej) ze szkoły średniej…
Nie narzekajmy jednak, tylko bierzmy się do roboty. W tym i w następnych postach pokażę Ci kilka szczegółów, których zrozumienie ułatwi bardzo całą naukę na studiach.
Zaczynamy od…
1. Interpretacja geometryczna wartości bezwzględnej (jako odległości)
O co chodzi tak z grubsza z tą wartością bezwzględną wszyscy wiemy. Nikt raczej nie ma problemu więc z tym, że:
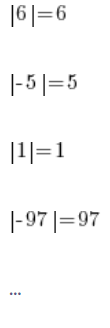
Operacja wartości bezwzględnej zwraca po prostu tą samą liczbę, a jeśli jest ona ujemna zmieniając jej znak na plus.
Co oznaczała by ona geometrycznie? Na osi liczbowej? Otóż po prostu odległość liczby od zera. Na przykład 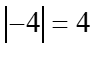 i rzeczywiście, bez wątpienia odległość liczby
i rzeczywiście, bez wątpienia odległość liczby ![]() od zera równa jest 4:
od zera równa jest 4:
Będziemy trzymać się dalej tego tropu i wartość bezwzględną rozumieć właśnie jako odległość.
Zauważmy jeszcze jedną rzecz:
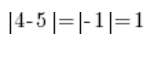
oraz, że na osi liczbowej:
…czyli że odległość pomiędzy 4 a 5 równa jest dokładnie wartości liczbowej z RÓŻNICY (odejmowania) 4 i 5, przy czym wszystko jedno, co odejmiemy od czego, bo:
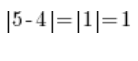
Tak samo jeśli odejmiemy od siebie na przykład liczby 3 i 8 i obliczymy z wyniku wartość bezwzględną otrzymamy dokładnie odległość na osi liczbowej pomiędzy liczbami 3 i 8 (będzie to 5).
Działa to także na liczbach ujemnych, na przykład -1 i 2:
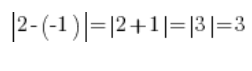
…czyli dokładnie odległość pomiędzy liczbami -1 i 2:
Możesz też pobawić się tym trochę sam. Jak masz jakiś podręcznik ze szkoły średniej zachęcam gorąco, żebyś przysiadł z godzinę nad tym tematem i trochę go porozwalał.
Możemy sformułować ogólną zasadę:
Wartość bezwzględna z różnicy (odejmowania) dwóch liczb: ![]() i
i ![]() równa jest odległości tych liczb od siebie.
równa jest odległości tych liczb od siebie.
Jak można więc rozszyfrować – na przykład – takie równanie:
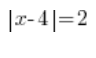
Wiemy, że fragment ![]() oznacza odległość niewiadomej x od 4, a z prawej strony równości wiemy, że ta odległość powinna być równa 2.
oznacza odległość niewiadomej x od 4, a z prawej strony równości wiemy, że ta odległość powinna być równa 2.
Rozwiązaniem równania będą więc liczby, których odległość od 4 równa jest 2, czyli liczby 2 i 6:
A teraz weźmy taką nierówność:
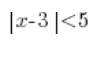
Jej lewa strona to odległość x od liczby 3, a czytając dalej otrzymujemy informację, że odległość ta powinna być mniejsza od 5. Tym razem rozwiązaniem tej nierówności nie będą dwie liczby tylko o wiele więcej – wszystkie liczby, których odległość od 3 jest mniejsza niż 5. Na osi wyglądało by to tak:
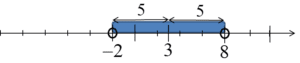
…czyli były by to wszystkie liczby od -2 do 8, czyli przedział liczbowy: ![]() . Odległość każdej takiej liczby od 3 jest mniejsza niż 5.
. Odległość każdej takiej liczby od 3 jest mniejsza niż 5.
Ten przedział liczbowy można też nazwać pewnym otoczeniem punktu 3 (ważne określenie, na studiach często używa się tego słownictwa).
Rozumując tak samo, można wykombinować, jakie liczby spełniają nierówność ![]() …
…
Nie jest to w sumie jednak moim celem (zresztą już to miałeś w średniej, prawda 🙂 ?).
Dobrze jest natomiast rozumieć wartość bezwzględną jako odległość, bo występuje ona w mnóstwie matematycznych definicji, z którymi zetkniesz się na studiach. I wtedy dobrze jest od razu wiedzieć, „o co kaman”.
Na przykład weźmy przytaczaną już wcześniej granicę ciągu:
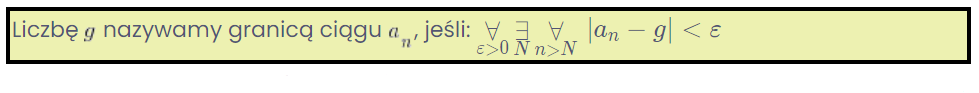
Skupmy się na razie na prawej stronie formuły. Krzaczki po lewej zostawmy do następnego postu.
Jakie jej odczytanie trafia bardziej do serca i jest lepiej zrozumiałe:
„wartość bezwzględna z różnicy ![]() i
i ![]() musi być mniejsza od
musi być mniejsza od ![]() ”
”
czy:
„odległość pomiędzy ![]() i
i ![]() musi być mniejsza od
musi być mniejsza od ![]() ”
”
?
Formalnie oba sposoby sformułowania definicji są równoważne, ale ten drugi jest prostszy i skupia się na istocie rzeczy, nie rozpraszając się niepotrzebnie jakimiś operacjami arytmetycznymi w stylu różnicy.
Rozumiejąc wartość bezwzględną jako odległość będzie Ci o wiele łatwiej zrozumieć mnóstwo – z pozoru skomplikowanych – matematycznych twierdzeń i definicji na studiach.
Co dalej?
W kolejnym poście zajmę się tymi dziwnymi znaczkami: ![]() i
i ![]() , więc będziemy już mogli zrozumieć w pełni całą naszą przykładową definicję.
, więc będziemy już mogli zrozumieć w pełni całą naszą przykładową definicję.


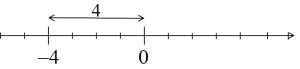

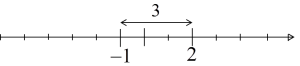
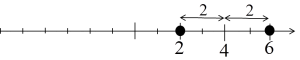

10 Komentarzy
Wodzu
Poprawka – wstawiłem zły kwantifikator.
Oczywiście rozwiązaniem równania jest:
[pmath] x=1 v x=3 [/pmath]
Krystian Karczyński
Zgadza się, tylko że ’ v ’ to nie jest „kwantyfikator”, tylko operator logiczny „lub”.
Ogólnie wielkie dzięki za czujność.
Anka
I2x-4I=2
2x=2-4 (różnica) 2x=2+4 (suma)
2x=-2 2x=6
x=-1 x=3
i w czym tkwi moje złe rozumowanie ?
Dziękuję za indywidualne podpowiedzi ale po prostu lubię rozumieć więc proszę się nie martwić bo „zadręczam” pytaniami nie tylko Pana 🙂
Krystian Karczyński
Jeśli takie jest rozumowanie, to jest ono jak najbardziej poprawne. Właściwie doszliśmy tu do znanej własności wartości bezwzględnej:
|COŚ|=a (a nieujemne)
COŚ=a lub COŚ=-a
Chociaż w poście bardziej o to mi chodziło, żeby rozumieć wartość bezwzględną jako odległość, a nie jak rozwiązywać związane z nią równania.
Uwielbiam dobre pytania 🙂
Wodzu
Z tym że rozwiązaniem równania:
[pmath] delim{|}{2x-4}{|}=2[/pmath]
jest:
[pmath] x=1 wedge x=3 [/pmath]
Tak więc rozumowanie do końca poprawne nie jest…
Krystian Karczyński
Też prawda.
Rozumowanie było w sumie O.K., bo było w nim „różnica pomiędzy wiadomą a wynikiem”.
W przykładzie |2x-4|=2 wiadomą było jednak 4, a wynikiem 2, czyli powinno być:
2x=4-2 (a nie 2x=2-4 , bo to by była „różnica pomiędzy wynikiem a wiadomą”)
2x=2
x=1
Anka
A mogłabym prosić o „skomplikowanie” ? Jakoś muszę to zobaczyć by „uwierzyć” w tą rozsypkę 😉
Krystian Karczyński
Jasne, na przykład zamiast prostego:
[pmath]delim{|}{x-4}{|}=2[/pmath]
…gdzie rozwiązanie równania to rzeczywiście różnica i suma 2 i 4, można by wziąść:
[pmath]delim{|}{2x-4}{|}=2[/pmath]
Anka
Czyli rachunkowo, mając w głowie wizualny sens wartości bezwzględnej, jest to różnica między wiadomą a wynikiem i suma między wiadomą a wynikiem ? Przy czym, rozwiązanie w nierównościach, niewiadoma większa od różnicy i niewiadoma mniejsza od sumy ?
Krystian Karczyński
Dzięki za pytanie 🙂
Rozwiązanie równania z wartością bezwzględną jako różnica i suma „wiadomej” a „wyniku”? No może i tak wychodzi, ale zdecydowanie lepiej się uczyć obrazowo poprzez te odległości, rysować je sobie na osiach itd.
Poza tym trzeba jeszcze koniecznie pamiętać, że zaproponowana przez Panią suma i różnica to nie jest wartość bezwzględna, tylko rozwiązanie pewnego szczególnego równania (wystarczy je zresztą lekko skomplikować i cały schemat się sypie).