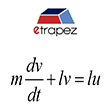
Jak rozwiązać równanie różniczkowe w fizyce? (VIDEO)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Matematykę używamy nie tylko na matematyce, oczywiście. Równania różniczkowe, na przykład, czekają na nas już za rogiem w fizyce, czy mechanice.
Oto jedno z nich:
Dzięki i powodzenia z fizyką na studiach!
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










Super
Też nie jestem fizykiem ale chyba:
m – masa
v(t) – prędkość
m * dv/dt = m*a = F – siła działająca na ciało
l*v(t) – też musi mieć wymiar siły, wygląda na składnik hamujący proporcjonalny do prędkości czyli siła tarcia
l*u – też musi mieć wymiar siły, więc u musi mieć wymiar prędkości i najprawdopodobniej będzie też zależeć od czasu czyli u(t), więc jest to jakaś prędkość przyśpieszająca ciało z współczynnikiem tarcia “l”
Lub można to zapisać tak:
m*dv/dt=m*a=F=l*(u(t)-v(t)) – w takim wypadku “l” może być współczynnikiem tarcia (np. gąsienicy czołgu o jezdnie ), przy czym obiekt porusza się z poślizgiem, np czołg hamujący (wtedy u(t) jest prędkością gąsienic (podzieloną przez 2) względem czołgu: jeżeli gąsienice są zablokowane wtedy u(t)=0)
Wow, dzięki! Tylko z tym uby się nie zgadzało, bo to miała być stała, a nie jakaś inna funkcja zależna od t…
Czy są “niezbędne wzory” na blogu w pdf tak jak np.z całek wielokrotnych?
Panie Krystanie, a będzie kiedyś kurs z matematyki dyskretnej, z równań różnicowych (rekurencyjnych)? Wielu studentów politechniki na pewno potrzebuje tego, tak samo jak ja:)
Może kiedyś będzie, ale na razie się nie szykuje…