Kilka rzeczy, których powinieneś się dobrze nauczyć w średniej, ale nikt Ci tego nie powiedział – część 4 Pierwiastek z x do kwadratu
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
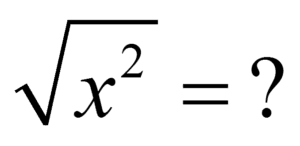 Dzisiaj będzie króciutko. Moje szybkie pytanie do Ciebie to:
Dzisiaj będzie króciutko. Moje szybkie pytanie do Ciebie to:
Ile to jest pierwiastek z x do kwadratu?
Czyli:
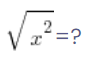
Kiedy udzielałem jeszcze korepetycji zadałem to pytanie naprawdę wielu studentom i uczniom szkół średnich. Czy wiesz, ilu znało prawidłową odpowiedź?
Dwóch.
Statystyka odpowiedzi rozkładała się z grubsza następująco:
75% odpowiadało, że ![]() (odpowiedź nieprawidłowa)
(odpowiedź nieprawidłowa)
20% wyczuwało już pułapkę i w ogóle bało się coś powiedzieć
5% wymyślało jakieś ciekawe i zaskakujące rzeczy
Przypadki dwóch uczniów znających prawidłową odpowiedź pomijam (przypadają oni na 7-8 lat intensywnych korepetycji).
Odpowiedź
Naprawdę nie wiem, czemu nikt tego nie wie, ale pierwiastek z x do kwadratu to jest wartość bezwzględna z x:
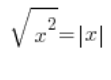
Gdyby miał to być x, to znaczy gdyby miało by zachodzić:
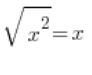
To znaczy, że jeśli za x wzięlibyśmy sobie (-1), powinniśmy dostać:
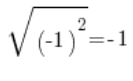
…a jakoś nie dostajemy, tylko dostajemy:
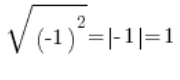
Z tą pułapką zetkniesz się nie raz na studiach i trzeba być czujnym. Moich uczniów nie pytałem zresztą dlatego, żeby robić sobie prywatne ankiety (w czasie, za który przecież oni płacili), tylko dlatego, że kwestia co chwila wypływała przy okazji różnych tematów.
No dobra, ale po co to? – przykład
Na przykład w granicach funkcji (ciągów zresztą też), trzeba często robić taki myk:
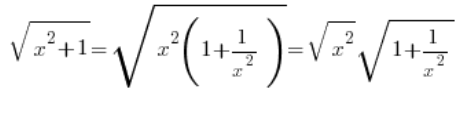
…no i standardowy babol tutaj to automatyczne:
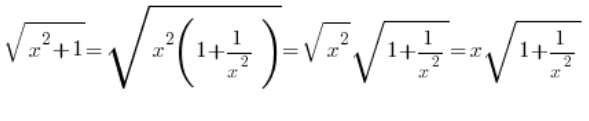
…co może, ale nie musi być prawdą, bo POWINNO być:
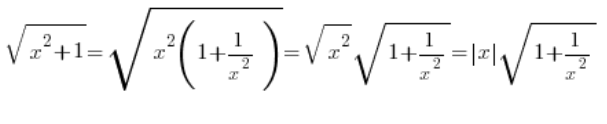
…teraz POWINNIŚMY sprawdzić, czy x jest dodatnie, czy ujemne (jeżeli jesteśmy w granicach i wiemy na przykład, że ![]() , to wiemy, że jest dodatni i to dodatni jak cholera).
, to wiemy, że jest dodatni i to dodatni jak cholera).
Teraz korzystając z definicji wartości bezwzględnej:
…wiemy, że jeśli x jest dodatni (no dobra: nieujemny) , to:
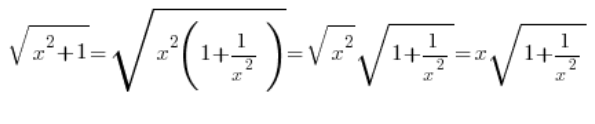
…ale jeśli x jest ujemny, to ku naszemu zaskoczeniu mamy:
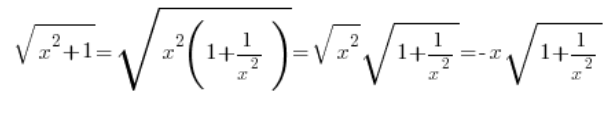
Pomyłka oczywiście najczęściej wpływa na wynik i na końcową punktację na kolokwium.
Uwaga zatem na ![]() !
!
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.










proste, |x|
Dobre!:)