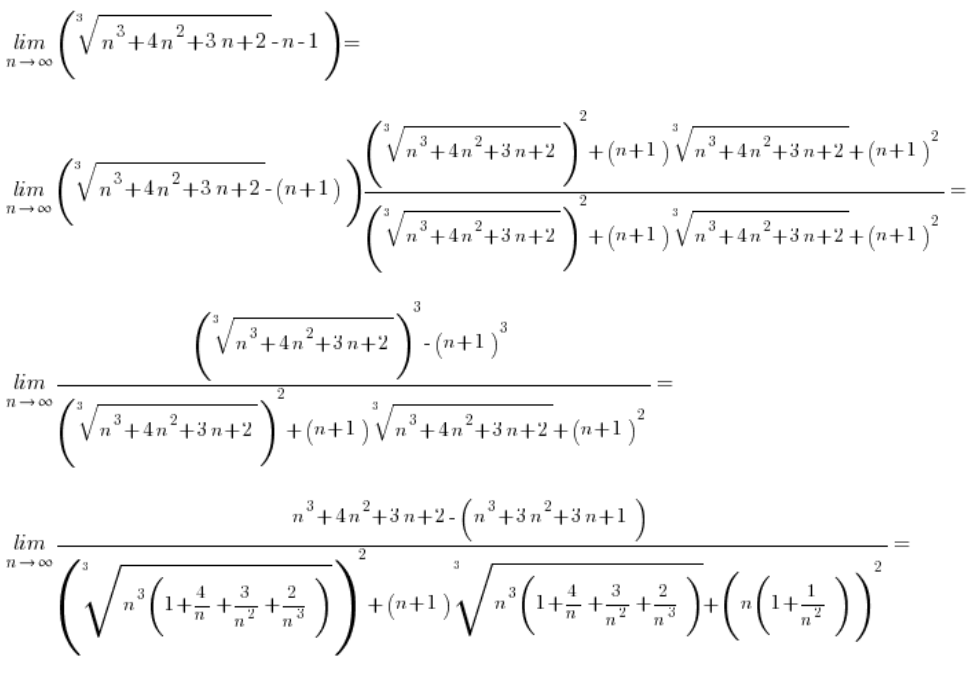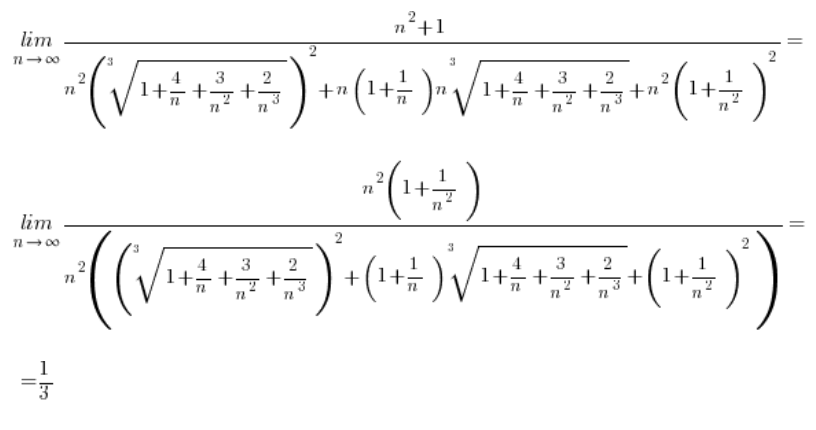“साधारण” मूलों के साथ यह कैसा दिखता था?
जब हमें एक सीमा की गणना करनी होती थी, जिसमें किसी प्रकार का घटाव और मूल शामिल होता था (और जिसे स्पष्ट रूप से सरलता से गणना नहीं की जा सकती थी), जैसे:
“कुछ – किसी चीज का मूल”
“किसी चीज का मूल – कुछ”
“किसी चीज का मूल – किसी चीज का मूल”
हम एक चाल का उपयोग करते थे, जिसे मैं “संयुग्मित से गुणा” कहता हूँ।
हम बस इस अभिव्यक्ति को उसके प्लस चिह्न वाले समकक्ष से गुणा करते थे, या अधिक सटीक रूप से, एक भिन्न से जिसमें यह समकक्ष अंश और हर में होता था।
उदाहरण के लिए:
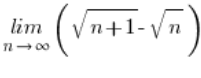 हम इस तरह से गुणा करते थे:
हम इस तरह से गुणा करते थे: 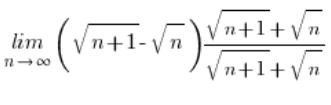
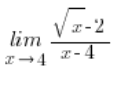 हम इस तरह से गुणा करते थे:
हम इस तरह से गुणा करते थे: 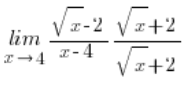
यह चाल हमें संक्षेप गुणा सूत्र तक पहुँचने की अनुमति देती थी:
![]()
इस सूत्र तक पहुँचने के बाद, वर्गमूल “काट” देते थे और हम सीधे उत्तर तक पहुँच जाते थे (ठीक है, कहें कि कभी-कभी थोड़ा लंबा सीधे उत्तर)।
लेकिन जब घटाव में शामिल मूल तीसरी शक्ति के होते हैं तो स्थिति कैसी होती है? उदाहरण के लिए यहाँ:
\underset{x\to 8}{\mathop{\lim }}\,\frac{\sqrt[3]{x}-2}{x-8}मानक प्रक्रिया, अर्थात निम्नलिखित तरीके से गुणा करना:
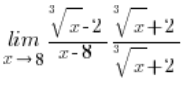
हमारे लिए कुछ भी नहीं करेगा, क्योंकि इस बार अंश में, सूत्र तक पहुँचने के बाद:
![]()
वर्ग किसी भी तरह से तीसरी शक्ति के मूलों को “काट” नहीं देगा। तो हम अभी भी वहीं रहेंगे।
तीसरी शक्ति के मूलों के साथ यह कैसा दिखेगा?
तीसरी शक्ति के मूलों के साथ घटाव के मामले में, हमें बस एक पूरी तरह से अलग सूत्र की ओर “लक्ष्य” करना होगा (लेकिन यह भी मध्य विद्यालय का है), अर्थात:
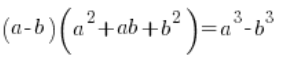
तो हमारे दिए गए ![]() (जहाँ a या b या दोनों तीसरी शक्ति के मूल हैं) को गुणा करने के बजाय
(जहाँ a या b या दोनों तीसरी शक्ति के मूल हैं) को गुणा करने के बजाय ![]() हम गुणा करेंगे
हम गुणा करेंगे ![]() और सूत्र को लागू करने के बाद, घनों को उनकी कार्यवाही करने देंगे, मूलों को “काट” देंगे।
और सूत्र को लागू करने के बाद, घनों को उनकी कार्यवाही करने देंगे, मूलों को “काट” देंगे।
उदाहरण 1
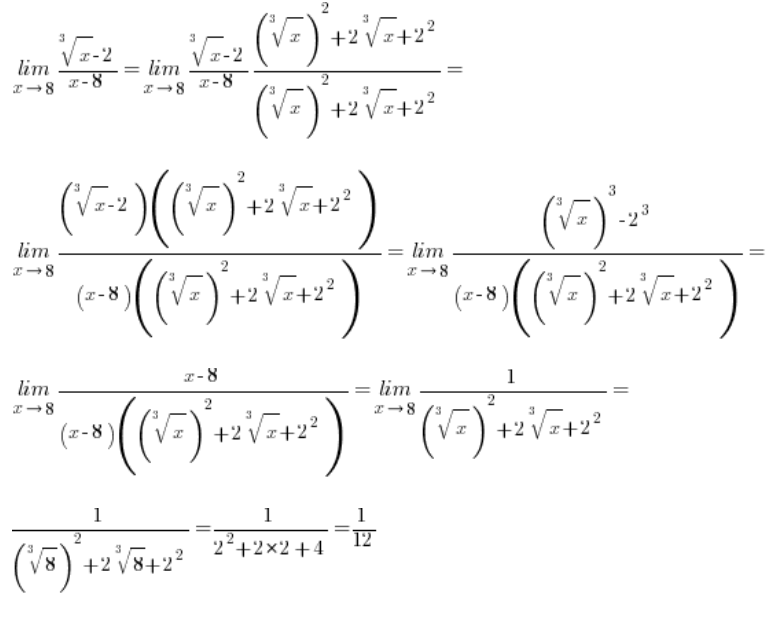
उदाहरण 2