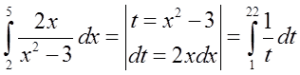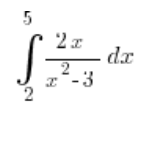
ऊपर दिखाई गई समस्या को निश्चित समाकलन के लिए हल करने के लिए हमें प्रतिस्थापन 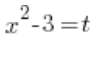 का उपयोग करना होगा, और हम सभी इस बात पर सहमत हैं। लेकिन समाकलन की सीमाओं का क्या?
का उपयोग करना होगा, और हम सभी इस बात पर सहमत हैं। लेकिन समाकलन की सीमाओं का क्या?
निश्चित समाकलन में प्रतिस्थापन कार्यों की सीमाएँ
क्या हम लिख सकते हैं:
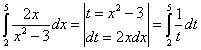 ?
?
बिलकुल नहीं। समाकलन की सीमाओं का मुद्दा। बाईं ओर के निश्चित समाकलन में, ये चर ![]() से संबंधित हैं, और दाईं ओर चर
से संबंधित हैं, और दाईं ओर चर ![]() से, इसलिए उन्हें भी चर के साथ बदलना चाहिए।
से, इसलिए उन्हें भी चर के साथ बदलना चाहिए।
एक समाधान (जिसे मैं अपने कोर्स में सलाह देता हूँ) यह है कि समस्या को पूरी तरह से नजरअंदाज करें, अनिर्धारित इंटीग्रल (इंटीग्रेशन की सीमाओं के बिना) को अलग से हल करें और बाद में परिणाम में (चर x के साथ) इंटीग्रेशन की सीमाएं 5 और 2 डालें।
दूसरा समाधान समस्या का सामना करना और प्रतिस्थापन के अनुसार इंटीग्रेशन की सीमाओं को बदलना है। चूँकि x चर की सीमाएँ 2 और 5 हैं, प्रतिस्थापन के बाद: 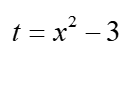 वे t चर में क्रमशः 1 और 22 होंगी, और मैंने ये परिणाम x के लिए 2 और 5 को प्रतिस्थापन
वे t चर में क्रमशः 1 और 22 होंगी, और मैंने ये परिणाम x के लिए 2 और 5 को प्रतिस्थापन 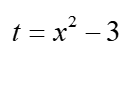 में डालकर प्राप्त किए। इसलिए सही कदम होगा:
में डालकर प्राप्त किए। इसलिए सही कदम होगा: