यह पोस्ट एक हाई स्कूल परीक्षा के सवाल के अंश को समर्पित है, जिसे एक हाई स्कूल के छात्र ने मुझे ईमेल के माध्यम से भेजा था। लेकिन जिज्ञासा से इसे देखना और फिर कभी यह नहीं कहना कि विश्वविद्यालय में गणित हाई स्कूल के एडवांस्ड गणित से कठिन है, एक अच्छा विचार है।
🙂
सवाल का हिस्सा
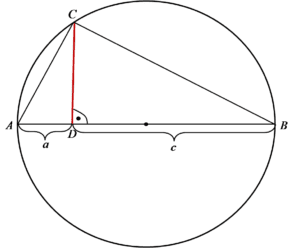
हमारे पास निम्नलिखित स्थिति है:
हमें दिखाना है कि लाल रंग से चिह्नित खंड की लंबाई 
है। यह पूरी सवाल का केवल एक छोटा सा हिस्सा है। अंदाज़ा लगाएं कि यह किस पर है? सीरीज पर है, बेशक 🙂
तो, यहां हम एक ट्रिक का उपयोग कर सकते हैं जो अक्सर त्रिभुज की ऊंचाई के सवालों में उपयोग होती है – समकक्ष त्रिभुज, जो सभी हाई स्कूल के छात्रों के “पसंदीदा” होते हैं।
1. त्रिभुज 
(सबसे छोटा) और 
(सबसे बड़ा, वृत्त में अंकित) समान होते हैं (उनके 2 समान कोण होते हैं: समकोण और <DAC, इसलिए तीसरा कोण भी समान होता है, जो हमें AA समानता देता है)। त्रिभुज 
(मध्यम) और (फिर से सबसे बड़ा) भी समान होते हैं (उनके 2 समान कोण होते हैं: समकोण और <CBD, इसलिए तीसरा कोण भी समान होता है, जो हमें फिर से AA समानता देता है)। यदि त्रिभुज और के समान हैं, तो वे भी एक दूसरे के समान होते हैं, और यही हम नोटिस करते हैं:
समान है
2. अगर ये त्रिभुज समान हैं, तो संबंधित पक्षों के अनुपात समान होंगे। बेशक, हम उन अनुपातों को चुनते हैं जिनमें लाल रंग से चिह्नित खंड होता है, जिसकी लंबाई हम 
के रूप में मानते हैं।
त्रिभुज में, सबसे छोटे पक्ष का मध्यम पक्ष के साथ अनुपात समान होगा:
त्रिभुज में, सबसे छोटे पक्ष का मध्यम पक्ष के साथ अनुपात समान होगा:
क्योंकि त्रिभुज समान हैं, एक समता होती है:
3. इस समता से, हम h निकालते हैं, जो लाल रंग से चिह्नित खंड की लंबाई है। हम अनुपातों की तरह क्रॉस गुणा करते हैं और प्राप्त करते हैं:
इसका मतलब है:
यानी हमने जो शुरुआत में दिखाना था वह सही साबित हुआ। बिंगो।
मोरल यह है: जब एक समकोण त्रिभुज में ऊंचाई निकाल रहे हों (जो कर्ण पर गिरती है बिल्कुल), तो अक्सर हमें त्रिभुज की समानता का उपयोग करना पड़ता है, जैसा कि ऊपर दिखाया गया है।
और एक और मोरल यह है कि उच्च विद्यालय में एडवांस्ड गणित वास्तव में कठिन हो सकती थी। केवल विश्वविद्यालय में हम वास्तव में आराम से सांस ले सकते हैं 🙂
