मेरे कम्प्लेक्स संख्या पाठ्यक्रम में, कार्टेशियन (या: बीजगणितीय) रूप में वर्गमूल की गणना करते समय, मैंने एक तरीका दिखाया जिसमें पहले से मौजूद दो समीकरणों के सेट में तीसरी समीकरण जोड़ने की विधि शामिल है, जो आगे की गणनाओं को बहुत ही सरल और छोटा कर देता है।
मैंने इस तरीके को दिखाया, लेकिन इसे किसी भी प्रकार से उचित नहीं ठहराया।
और हाल ही में मुझे इस विषय पर एक ईमेल प्राप्त हुआ:
नमस्ते
क्या आप समझा सकते हैं कि हम कम्प्लेक्स संख्या के वर्गमूल की गणना करते समय तीसरी समीकरण जोड़ने की विधि का उपयोग क्यों कर सकते हैं?
x^2 + y^2 = उस संख्या का मापांक जिसका हम वर्गमूल निकाल रहे हैं
यह एक बहुत ही अच्छा सवाल है और गणित में वास्तव में वे धन्य हैं जो प्रोफेसरों की बातों पर सीधे विश्वास नहीं करते, बल्कि हमेशा पूछते हैं: “यह कहां से आया?” 🙂
यथार्थता
तो अब मुझे केवल एक संभावित तरीके से इस विधि को उचित ठहराना है:
वर्गमूल की गणना के पहले कुछ चरणों के बाद, हमारे पास यह स्थिति है:
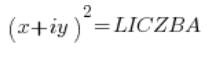
चूंकि बाईं और दाईं तरफ की संख्याएं (मैं हर बार “कम्प्लेक्स संख्या” नहीं लिखूंगा) बराबर हैं, इसलिए उनके मापांक भी बराबर होने चाहिए (उल्टा सही नहीं है, लेकिन यह महत्वपूर्ण नहीं है), यानी:
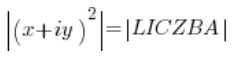
संख्या का वर्ग संख्या को उसके आप में गुणा करने के बराबर है, यानी:
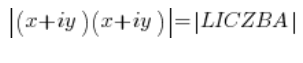
कम्प्लेक्स संख्या के मापांक की एक विशेषता है: 
, इसलिए बाईं तरफ हम लिख सकते हैं:
… और बाईं तरफ मापांक की गणना करते समय हमारे पास है:
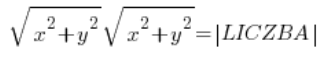
यानी:
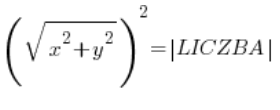
यानी:
यानी:
बिंगो
अच्छे सवाल के लिए धन्यवाद!
