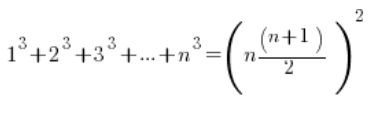क्रमों की सीमाओं में, कभी-कभी ऐसा होता है:
![]()
और कभी-कभी ऐसा भी होता है:
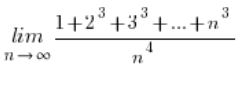
तब क्या करें?
उत्तर सरल है:
लगातार प्राकृतिक संख्याओं के वर्गों के योग और घनों के योग के सूत्र।
ये इस प्रकार हैं:
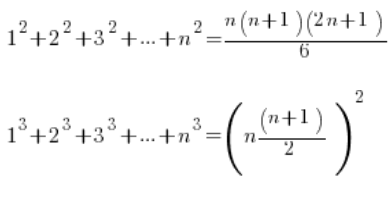
सूत्र – जैसे कि कोई भी सूत्र – याद करने के लिए होते हैं। यदि आपके पास इसी प्रकार के उदाहरण हैं और आपको इनकी आवश्यकता है।
इन सूत्रों को जानने के बाद, हमारी सीमाओं की गणना बहुत आसान हो जाती है:
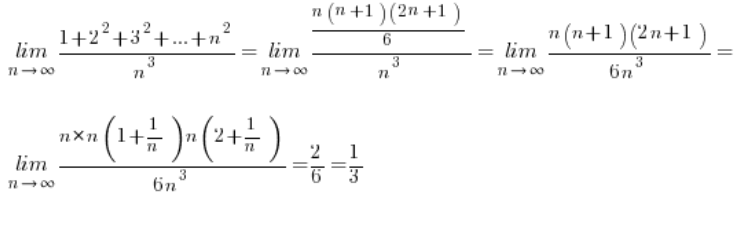
अगली सीमा:
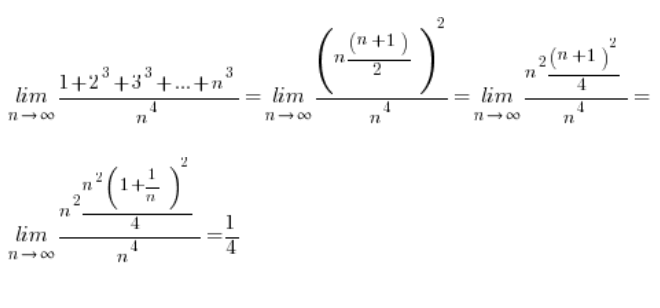
सूत्रों के लिए संकेतक प्रमाण
सूत्रों की सत्यता को आसानी से संकेतक विधि द्वारा प्रमाणित किया जा सकता है (कम से कम कुछ साल पहले तक यह स्कूल में पूरी तरह से मानक था)। मैं इस सूत्र के लिए ऐसा करूंगा:
1. 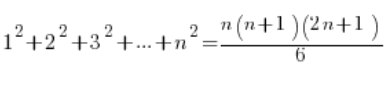
संकेतक का पहला चरण
हम n=1 के लिए सूत्र की सत्यता की जांच करते हैं:
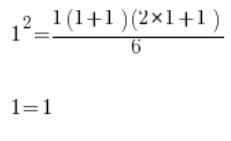
यह सही है
संकेतक का दूसरा चरण
हम मान लेते हैं परिकल्पना, कि किसी प्राकृतिक n के लिए:
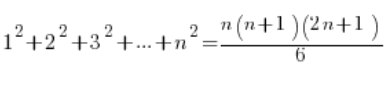
संकेतक का तीसरा चरण
हम थिसिस को प्रमाणित करते हैं (स्वीकृत परिकल्पना का उपयोग करके), कि n+1 के लिए सूत्र भी सही है, अर्थात:
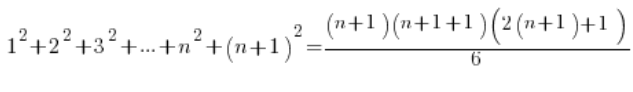
बाईं ओर ![]() के बजाय हम परिकल्पना से सूत्र डालते हैं, और दाईं ओर हम बस व्यवस्थित करते हैं:
के बजाय हम परिकल्पना से सूत्र डालते हैं, और दाईं ओर हम बस व्यवस्थित करते हैं:
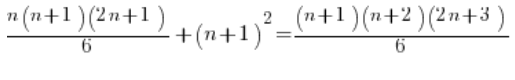
और फिर मजबूरी में न करते हुए, हम थोड़ा सूक्ष्म तरीके से काम करते हैं:
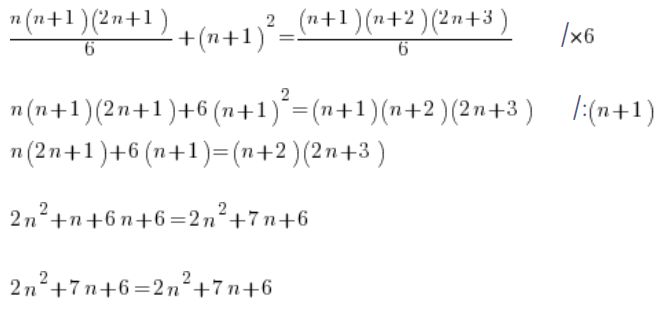
अर्थात, थिसिस प्रमाणित हो गई। सूत्र संकेतक विधि से प्रमाणित हो गया।
मैं आपको आमंत्रित करता हूं कि आप घनों के योग के लिए दूसरे सूत्र को संकेतक विधि से प्रमाणित करें: