यूलर प्रतिस्थापन का दूसरा प्रकार

---

यूलर प्रतिस्थापन का पहला प्रकार (a>0 के लिए) – पुनरावृत्ति

पिछली पोस्ट में:

यूलर प्रतिस्थापन का पहला प्रकार

हमने इस प्रकार के समाकलों का अध्ययन किया:

,

जिसमें a>0 है।

हमने एक उदाहरण समाकल भी हल किया, जो इस शर्त को पूरा करता है, अर्थात

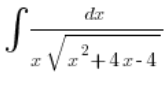
लेकिन क्या हो अगर त्रिपद में ऋणात्मक हो (a=0 की स्थिति को नजरअंदाज किया जा सकता है क्योंकि तब यह द्विघात त्रिपद नहीं होगा और समाकल को सरल प्रतिस्थापन के माध्यम से हल किया जा सकता है यूलर प्रतिस्थापन से अधिक) ?

तब दूसरा प्रकार का यूलर प्रतिस्थापन हमारी मदद कर सकता है (लेकिन जरूरी नहीं…):

यूलर प्रतिस्थापन का दूसरा प्रकार (c>0 के लिए)

हमारे पास इस प्रकार का समाकल है:

,

जिसमें c>0 है, हम इस प्रकार का प्रतिस्थापन उपयोग करते हैं:

,

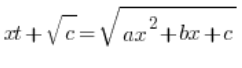जिसे हम फिर से दोनों पक्षों को वर्ग करते हैं, जिसमें इस बार वाले तत्व घट जाते हैं और हमें दोनों पक्षों को से विभाजित करना होता है, ताकि हमें एक रैखिक संबंध मिले, जिससे हम चर की सहायता से हल करें:

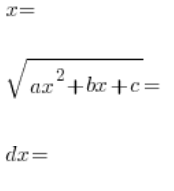
हम इसे समाकल में डालते हैं:

और हम फिर से एक यौक्तिक समाकल प्राप्त करते हैं, जो – मैं दोहराता हूं – आम तौर पर थकाऊ है।

तो चलिए एक उदाहरण से शुरू करते हैं।

उदाहरण

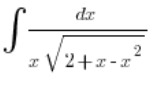
द्विघात त्रिपद में तत्वों का क्रम थोड़ा बदला हुआ है, लेकिन यह स्पष्ट है कि । इसका मतलब है कि से बड़ा नहीं है (इसलिए हम यूलर के पहले प्रकार का प्रतिस्थापन नहीं उपयोग करेंगे), लेकिन c>0 है (इसलिए हम दूसरे प्रकार का उपयोग करेंगे)।

हम प्रतिस्थापन करते हैं:

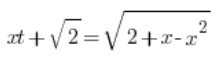
दोनों पक्षों को वर्ग करते हैं:

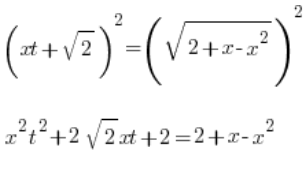
तत्व 2 घट जाता है (ऐसा ही होना चाहिए):

और अब कुछ ऐसा, जो पहले प्रकार के प्रतिस्थापन में नहीं था, हम दोनों पक्षों को x से विभाजित करते हैं:

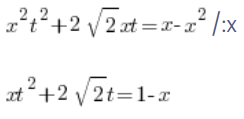
फिर हम x के लिए हल करते हैं:

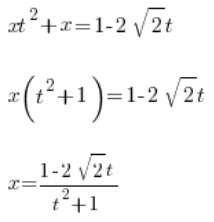
हमने x को चर t के माध्यम से हल किया है। अब हम 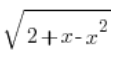के लिए हल करते हैं। शुरू में हमारा प्रतिस्थापन था:

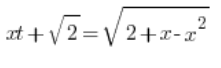
पहले से हल किया गया है, इसलिए हम इसे केवल डालते हैं:

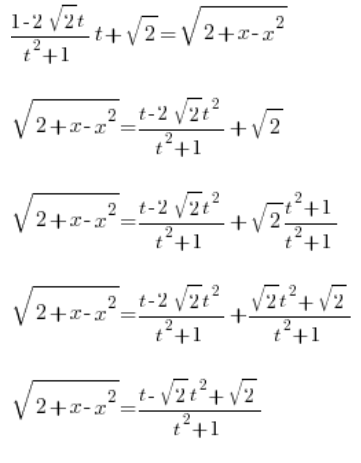
हमें केवल के लिए हल करना है। हम इसे का अवकलन लेकर गणना करते हैं:

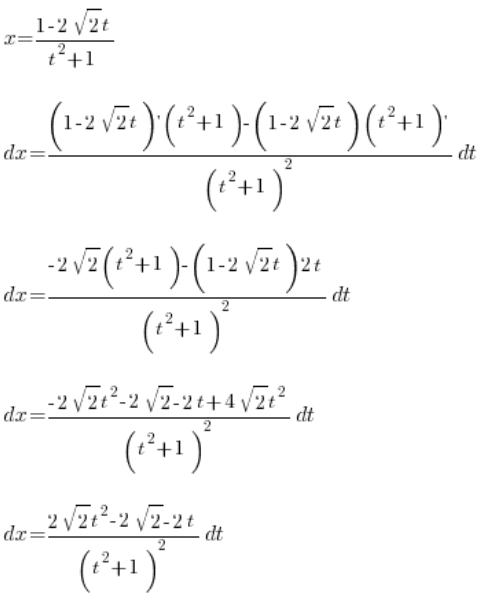
इस प्रकार हमने हल किया है:

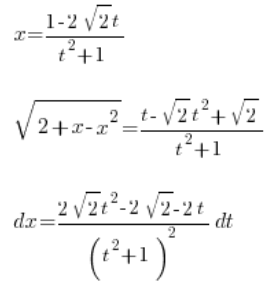
, सब चर का उपयोग करके। हम समाकल लेते हैं:

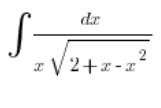
और प्रतिस्थापित करते हैं:

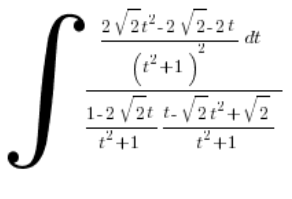
चलो सफाई करते हैं:

\int{\frac{-2\left( -\sqrt{2}{{t}^{2}}+\sqrt{2}+t \right)}{\left( 1-2\sqrt{2}t \right)\left( -\sqrt{2}{{t}^{2}}+\sqrt{2}+t \right)}dt} \int{\frac{-2}{1-2\sqrt{2}t}dt}=\left| \begin{matrix}&u=1-2\sqrt{2}t\\&du=-2\sqrt{2}dt\\&dt=\frac{du}{-2\sqrt{2}}\\\end{matrix} \right|=\int{\frac{-2}{u}\frac{du}{-2\sqrt{2}}}=\frac{1}{\sqrt{2}}\int{\frac{du}{u}}=\frac{1}{\sqrt{2}}\ln \left| u \right|+C

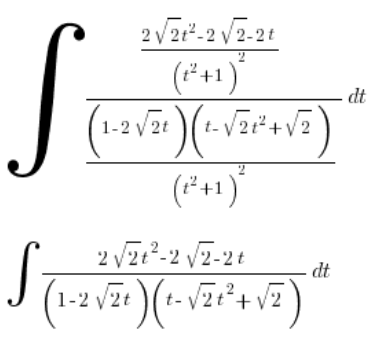
प्रतिस्थापन पर वापस:

\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C

हमें अभी भी t से x पर लौटना है। हमारा यूलर प्रतिस्थापन था

xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}

जिससे

t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}

इस प्रकार हमारा समाधान है

\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+C

अन्य मामलों का क्या?

हम जानते हैं कि जब समाकल में:

• a>0 – हम पहले प्रकार का प्रतिस्थापन उपयोग करते हैं
• c>0 – हम दूसरे प्रकार का प्रतिस्थापन उपयोग करते हैं

लेकिन अगर न तो और न ही शून्य से बड़े हैं? हम इसे अगले पोस्ट में चर्चा करेंगे, जिसमें मैं यूलर प्रतिस्थापन के तीसरे प्रकार को कवर करूंगा और दिखाऊंगा कि विषय समाप्त हो जाएगा, अर्थात, प्रत्येक प्रकार के समाकल के लिए:

…हम तीन प्रकार के प्रतिस्थापनों में से एक का चयन करेंगे।