No products in the cart.
Krystian Karczyński- 24 जून 2024
- Komentarz 0
हमारे पास एक फ़ंक्शन की सीमा है:
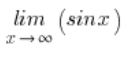
सहज रूप में हम महसूस करते हैं कि उपरोक्त सीमा मौजूद नहीं है। x मान बड़े और बड़े होते जा रहे हैं, और साइन मान हमेशा -1 और 1 के बीच “डोल” रहे हैं।
औपचारिक प्रमाण
लेकिन इसे औपचारिक रूप से कैसे प्रदर्शित और प्रमाणित करें?
परिभाषा से जब x अनंत की ओर बढ़ता है तो फ़ंक्शन की सीमा हम जानते हैं कि सीमा मौजूद है यदि हर तर्क की श्रृंखला जो 
की ओर बढ़ रही हो, उसके लिए फ़ंक्शन मूल्यों की श्रृंखला उसी संख्या की ओर अभिसरण करती है (फिर वह संख्या सीमा है)।
तो यह दिखाने के लिए कि ऐसी सीमा मौजूद नहीं है, बस दो किसी भी तर्कों की श्रृंखला लें जो की ओर बढ़ रही हो और दिखाएँ कि मूल्यों की श्रृंखला दो विभिन्न संख्याओं की ओर अभिसरण करती है।
हम जानते हैं कि साइन फ़ंक्शन आवर्तक है, इसलिए ये श्रृंखलाएँ उदाहरण के लिए हो सकती हैं:
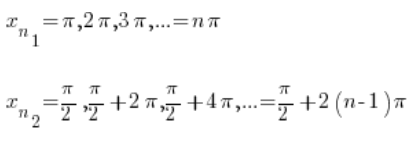
स्पष्ट रूप से, दोनों श्रृंखलाएँ अनंत की ओर बढ़ती हैं जब 
।
अब इन श्रृंखलाओं के संगत फ़ंक्शन मूल्यों की श्रृंखला देखें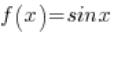 
:
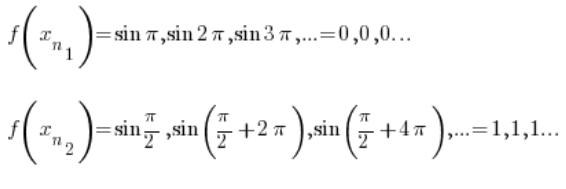
स्पष्ट रूप से, पहली श्रृंखला 0 की ओर अभिसरण करती है, और दूसरी श्रृंखला 1 की ओर।
यह साबित करने के लिए पर्याप्त है कि फ़ंक्शन की सीमा:
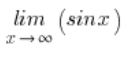
मौजूद नहीं है।
Related Posts
मैट्रिक्स की रैंक का “आँकड़ों से” अनुमान
Posted on
असंततियों के दो प्रकार (कार्य सीमा)
Posted on