No products in the cart.
Krystian Karczyński- 21 जून 2024
- Komentarz 0
मैट्रिक्स की रैंक की परिभाषा और इसके परिणाम
मान लेते हैं कि हमने मैट्रिक्स की रैंक को इस प्रकार परिभाषित किया है: “मैट्रिक्स में रैखिक स्वतंत्र पंक्तियों और स्तंभों की संख्या”। इस परिभाषा से प्रारंभ में ही कौन-कौन सी विशेषताएँ निकलती हैं?
सबसे पहले, यह स्पष्ट है कि मैट्रिक्स की रैंक 1, या 4, या कभी-कभी 0 हो सकती है। लेकिन यह निश्चित रूप से -4, या 
नहीं हो सकती।
अच्छा, क्या यही सब कुछ है?
लेकिन क्या यही सब कुछ है? उदाहरण के लिए, यह मैट्रिक्स देखें:
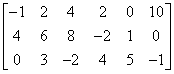
इस मैट्रिक्स में 3 पंक्तियाँ और 6 स्तंभ हैं।
आइए खुद से पूछें, इस मैट्रिक्स की रैंक क्या हो सकती है? क्या यह 7 हो सकती है? यह स्पष्ट है कि नहीं, क्योंकि अगर मैट्रिक्स की रैंक “रैखिक स्वतंत्र पंक्तियों और स्तंभों की संख्या” है, तो इस मामले में यह 7 नहीं हो सकती, क्योंकि इस मैट्रिक्स में इतने पंक्तियाँ या स्तंभ ही नहीं हैं!
अब एक कठिन सवाल… क्या रैंक 6 हो सकती है? इस मैट्रिक्स में 6 स्तंभ तो हैं…
उत्तर है: नहीं। 6 “रैखिक स्वतंत्र पंक्तियों और स्तंभों की संख्या” होनी चाहिए। 6 रैखिक स्वतंत्र स्तंभों की संख्या हो सकती है (क्योंकि 6 स्तंभ हैं), लेकिन रैखिक स्वतंत्र पंक्तियों की संख्या नहीं हो सकती (क्योंकि केवल 3 पंक्तियाँ हैं)। और इसे रैखिक स्वतंत्र “पंक्तियों और स्तंभों” की संख्या होनी चाहिए।
इसलिए, यह स्पष्ट है कि इस मैट्रिक्स की रैंक अधिकतम 3 हो सकती है।
हम एक उपयोगी गुण तक पहुँचते हैं:
रैंक(A) <= न्यूनतम (मैट्रिक्स में पंक्तियों की संख्या, मैट्रिक्स में स्तंभों की संख्या)
इसलिए, मैट्रिक्स को देखकर, आप तुरंत उसकी अधिकतम रैंक बता सकते हैं – जो कभी-कभी बहुत उपयोगी हो सकता है।
इसे अधिक सटीक रूप से गणना करने के लिए, आपको उपयुक्त विधियों का उपयोग करना होगा – मैं अपने मैट्रिक्स कोर्स में पाठ 5 में इन्हें दिखाता हूँ, स्वागत है!
