जब घातांक लगाना बिल्कुल नहीं हो रहा है तो क्या करें (संपूर्ण संख्याएँ)

---

कुछ दिन ऐसे होते हैं जब कुछ भी ठीक नहीं चलता।

और कुछ उदाहरण होते हैं जहाँ जटिल संख्याओं के साथ कुछ भी सही नहीं होता। जानी-पहचानी और याद की हुई विधियाँ मदद नहीं करतीं।

उदाहरण के लिए यह साधारण सा दिखने वाला घातांक:

{( 1+2i )^8}

बहुत सारे उदाहरणों में इस्तेमाल किए गए पुराने तरीके का पालन करते हुए, आप संख्या को त्रिकोणमितीय रूप में लिखना चाहते हैं और फिर इसे आठवीं शक्ति में उठाना चाहते हैं।

तो आप मापांक की गणना करते हैं:

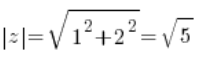
फिर आप प्रमुख तर्क का साइन और कोसाइन निकालते हैं:

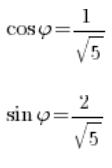
साइन और कोसाइन के संकेत सकारात्मक हैं, इसलिए कोण पहले चतुर्थांश में है, लेकिन आपकी किस्मत यहीं खत्म हो जाती है।

दुर्भाग्यवश, साइन और कोसाइन के मान: और आपको मूल त्रिकोणमितीय मानों की तालिका में नहीं मिलते। कोई आश्चर्य नहीं – कोण न तो 0 है, न 30, न 45, न 60, न 90 डिग्री।

तो समस्या है।

क्या किया जा सकता है?

ऐसी स्थिति जहाँ एक संख्या को घातांक में उठाया जाता है और आसानी से त्रिकोणमितीय रूप में नहीं बदला जा सकता, हो सकती है। दुर्भाग्यवश।

लेकिन किसी ने नहीं कहा कि वही संख्या जिसे वर्ग में उठाया गया है (उदाहरण के लिए) अभी भी “अपरिवर्तनीय” होगी।

तो इसे आजमाएं:

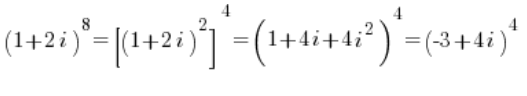
इसलिए आप संख्या: को त्रिकोणमितीय रूप में बदलने के बजाय संख्या को बदलते हैं…

दुर्भाग्यवश, समान खराब परिणामों के साथ, क्योंकि यद्यपि मापांक सुंदर और गोल है, साइन और कोसाइन के मान अभी भी तालिका से पढ़ने योग्य नहीं हैं।

अब क्या करें?

पुनः प्रयास करें 🙂

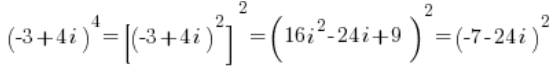
और यहाँ, त्रिकोणमितीय रूप में संघर्ष करने के बजाय, इसे बीजगणितीय रूप में वर्ग करें:

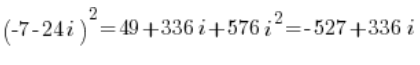
इस प्रकार, ध्यान दें, त्रिकोणमितीय रूप को छुए बिना (क्योंकि इसे नहीं किया जा सका), हमने अपेक्षाकृत उच्च शक्ति के जटिल संख्या की गणना की – मुझे लगता है अब भी दर्द रहित -:

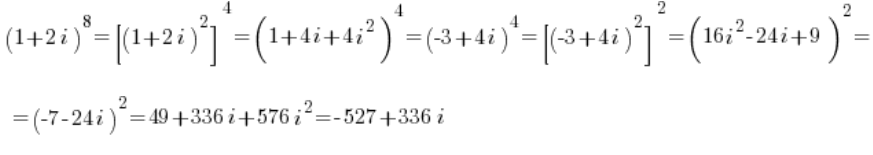
बिल्कुल। यह हमेशा “काम” नहीं करता। लेकिन कभी-कभी मदद कर सकता है, है न? 🙂