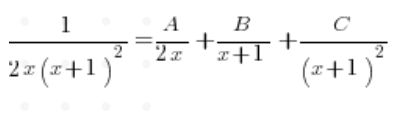गणन संपूर्ण अंक में डेल्टा शून्य के बराबर है

---

एक द्विघात त्रिपद को घटकों में विभाजित करना

तर्कसंगत अनिश्चित समाकल में, हमें अक्सर एक द्विघात त्रिपद को घटकों में विभाजित करने की आवश्यकता होती है: 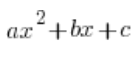। हम ऐसा करते हैं निश्चित रूप से सूत्र के माध्यम से: 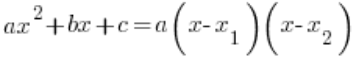, जो काम करता है जब ।

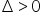तर्कसंगत समाकल और डेल्टा बराबर 0

लेकिन जब डेल्टा ठीक 0 होता है, तब यह द्विपद कैसा दिखता है? उदाहरण के लिए, यह घटक कैसे दिखेगा: ?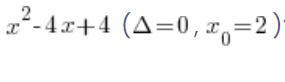

क्या ऐसा है:  ?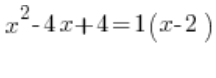

बिल्कुल नहीं… हाई स्कूल से हमें याद है कि अगर , तो हमें वास्तव में एक मूल मिलता है, लेकिन यह एक दोहरा मूल है। इसलिए हमारे उदाहरण में, हम कह सकते हैं: , जिसका मतलब है कि द्विघात त्रिपद को घटकों में विभाजित करने से यह दिखता है:

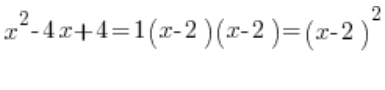
इसका तर्कसंगत अनिश्चित समाकल में काफी प्रभाव होता है जब इसे सरल अंशों में विभाजित किया जाता है।

उदाहरण

हम एक उदाहरण लेते हैं:

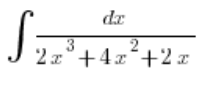
हम अंश को बिना समाकल के ही अलग करते हैं और लिखते हैं:

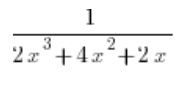
हम हर नीचे वाले पद से x को बाहर निकालते हैं:

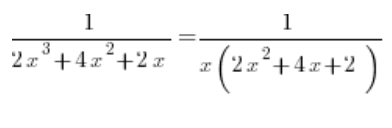
नीचे के द्विघात त्रिपद से डेल्टा की गणना की जाती है, जो 0 है, और हम पाते हैं कि मूल (-1) है। इसे घटकों में विभाजित करते हुए हम पाते हैं:

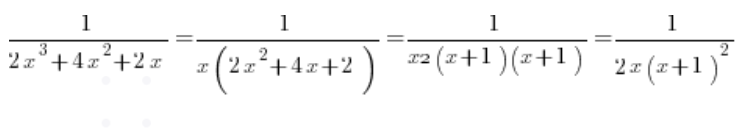
और इसे सरल अंशों में विभाजित करते हुए: