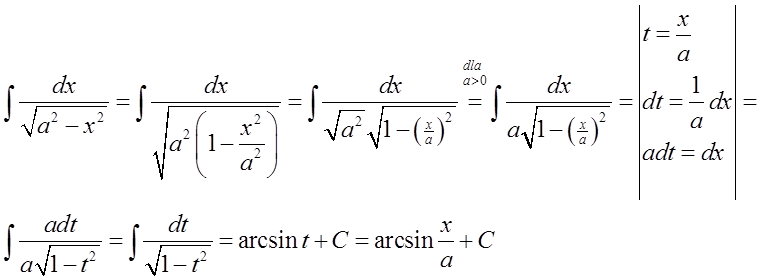विश्वविद्यालयों में प्रोफेसरों की अपनी-अपनी मांगें होती हैं। अपने छात्रों की भलाई के लिए, कई प्रोफेसर यह सुनिश्चित करने से पीछे नहीं हटते कि समस्याओं को हल करने के नियमों को बहुत विस्तार से निर्धारित किया जाए।
मेरे अनिश्चित समाकलन पाठ्यक्रम के एक उपयोगकर्ता ने मुझे GG पर लिखा:
मेरे पास एक अनुरोध है, क्या आप अपने फेसबुक या ब्लॉग पर दिखा सकते हैं कि आपके सूत्रों में समाकल को कैसे कागज पर दी गई रूप में लाया जाता है? मेरा मतलब सूत्र नंबर: 5, 9, 10, 13, 14, 15, 16 से है। दुर्भाग्य से हमारे प्रोफेसर ने हमें बताया कि केवल सबसे सरल को ही इस्तेमाल किया जा सकता है, मैंने जो अधिक जटिल सूत्र बताए हैं, उन्हें हमें स्वयं दिए गए रूप में तोड़ना होगा। मुझे लगता है कि बहुत से लोग आपके लिए इसके लिए आभारी होंगे 🙂
यह पाठ्यक्रम के साथ संलग्न सूत्र पत्रक के बारे में है:
और विशेष रूप से ये सूत्र:
5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}
10.\quad \int{ctgxdx=\ln \left| \sin x \right|}+C
13.\quad \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C}
14.\quad \int{\frac{dx}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{2a}\ln \left| \frac{x-a}{x+a} \right|+C}
15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}
16.\quad \int{\frac{dx}{\sqrt{{{x}^{2}}+q}}=\ln \left| x+\sqrt{{{x}^{2}}+q} \right|+C}
यदि ये नहीं, तो अन्य
हां, यह सच है, प्रोफेसर अक्सर मांग करते हैं कि इन विशिष्ट सूत्रों का उपयोग किया जाए, या कुछ सूत्रों का बिल्कुल भी उपयोग न किया जाए। या उन सूत्रों का उपयोग किया जाए जिन्हें हम उपयोग करना पसंद नहीं करते।
ऐसी स्थितियों में तर्कसंगत व्यक्ति के लिए एकमात्र तरीका पूरी तरह से अनुपालन करना है। परीक्षा हॉल में प्रोफेसर ही कानून है और यह शिकायत करने का कोई मतलब नहीं है कि प्रोफेसर ने कोलोक्वियम पास नहीं किया, हालांकि “उसे करना चाहिए था”।
इसके बजाय, मैं उल्लेखित सूत्रों की एक-एक करके समीक्षा करूंगा और दिखाऊंगा कि प्रत्येक मामले में व्यक्तिगत रूप से कैसे निपटा जाए (दुर्भाग्य से उन्हें किसी सामान्य नियम के तहत “समाहित” नहीं किया जा सकता)। “निपटना” का मतलब है उस सूत्र का उपयोग किए बिना उस सूत्र का उपयोग किए बिना, कम सामान्य सूत्र का उपयोग करके, या प्रतिस्थापन के माध्यम से, या तर्कसंगत तरीके से समाकल को हल करना।
तो, एक-एक करके:
5.\quad \int{{{a}^{x}}dx=\frac{{{a}^{x}}}{\ln a}+C}
इस सूत्र के साथ, वास्तव में मुझे समझ में नहीं आता कि समस्या क्या है, यह सीधे व्युत्पन्न सूत्र को उलटने से उत्पन्न होता है:
{{\left( {{a}^{x}} \right)}^{\prime }}={{a}^{x}}\ln aयहां मैं प्रोफेसर के सामने पूरी तरह से झुकता नहीं हूं, बल्कि इस बारे में स्पष्टीकरण मांगता हूं कि कृपया \int{{{3}^{x}}dx} की गणना कैसे करें, बिना \int{{{a}^{x}}dx} का उपयोग किए।
यदि किसी के पास कोई दिलचस्प विचार है, तो कृपया इसे पोस्ट के नीचे टिप्पणियों में मानवता के साथ साझा करें।
9.\quad \int{tgxdx=-\ln \left| \cos x \right|+C}
ठीक है, खेल में वापस आते हैं।
यह सूत्र सीधे किसी भी व्युत्पन्न सूत्र को उलटने से उत्पन्न नहीं होता है।
यदि हम सहमत हैं कि हम इसे नहीं जानते हैं, तो हम प्रतिस्थापन के माध्यम से समाकल \int{tgxdx} की गणना कर सकते हैं:
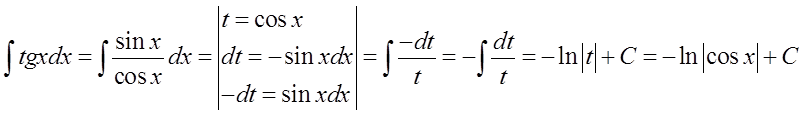
यहां पिछली तरह ही:
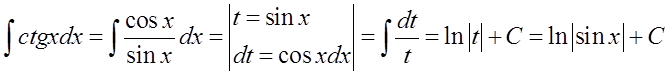
यह सूत्र निम्नलिखित सूत्र का सामान्य रूप है:
\int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} या: \int{\frac{dx}{1+{{x}^{2}}}=arctgx+C}
प्रोफेसर का मतलब है कि हमें सूत्र का उपयोग करना चाहिए: \int{\frac{dx}{{{x}^{2}}+1}=arctgx+C} (जो सरल व्युत्पन्न सूत्र को उलटने से उत्पन्न होता है), और सूत्र का उपयोग नहीं करना चाहिए: \int{\frac{dx}{{{x}^{2}}+{{a}^{2}}}=\frac{1}{a}arctg\frac{x}{a}+C} (जो पहले से ही एक “प्रसंस्कृत” सूत्र है)।
हम इसे इस प्रकार करते हैं (परिवर्तन और प्रतिस्थापन के माध्यम से):
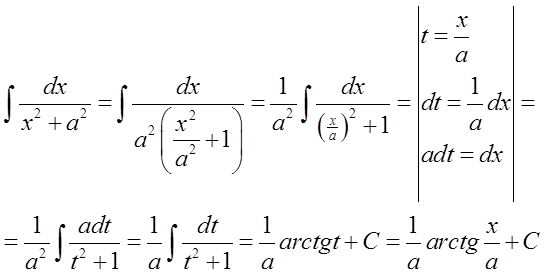
एक विशिष्ट उदाहरण में, यह इस तरह दिख सकता है:
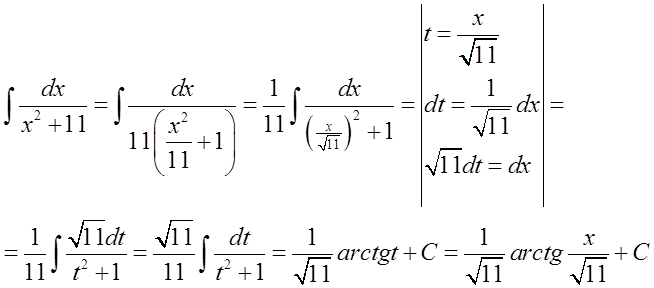
यह सूत्र पिछले एक से भिन्न है, इसका मतलब यह नहीं है कि किसी सूत्र का उपयोग किया जाए जिसमें ‘a’ की जगह ‘1’ हो (ऐसा कोई सूत्र नहीं है)। इस सूत्र का उपयोग करने का विकल्प यहाँ सरल भिन्नों में विभाजित करना है जैसे कि तर्कसंगत समाकल (मैंने दिखाया कि इसे अनिश्चित समाकल पाठ्यक्रम के पाठ 5 में कैसे किया जाता है)।
वास्तव में, \frac{1}{{{x}^{2}}-{{a}^{2}}}=\frac{1}{\left( x-a \right)\left( x+a \right)} और इसे आगे सरल भिन्नों में विभाजित किया जा सकता है। उदाहरण के लिए:
\frac{1}{{{x}^{2}}-9}=\frac{1}{\left( x-3 \right)\left( x+3 \right)} \frac{1}{\left( x-3 \right)\left( x+3 \right)}=\frac{A}{x-3}+\frac{B}{x+3}फिर हम \left( x-3 \right)\left( x+3 \right) से गुणा करते हैं, A, B स्थिरांक की गणना बहुपदों की तुलना करके करते हैं और सभी को पाठ 5 में दिखाया गया है पाठ्यक्रम।
15.\quad \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C}यहां फिर से सामान्य सूत्र: \int{\frac{dx}{\sqrt{{{a}^{2}}-{{x}^{2}}}}=\arcsin \frac{x}{a}+C} को विशेष सूत्र में परिवर्तित किया जाना चाहिए: \int{\frac{dx}{\sqrt{1-{{x}^{2}}}}=\arcsin x+C}।
हम इसे सूत्र 13 के समान करते हैं:
एक विशिष्ट उदाहरण में, यह इस तरह दिख सकता है:
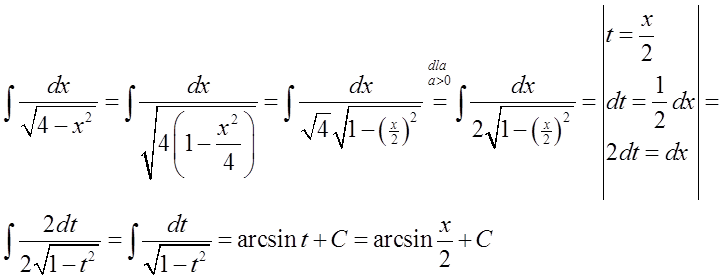
मामला अधिक जटिल है, इसमें तथाकथित “हाइपरबोलिक प्रतिस्थापनों” (हाइपरबोलिक साइन और कोसाइन) के उपयोग की आवश्यकता होती है। इस पोस्ट में मैं इस विषय को छोड़ रहा हूं, और जल्द ही निश्चित रूप से इन प्रतिस्थापनों के बारे में लिखूंगा।
ये वे सूत्र हैं जिनके बारे में उपयोगकर्ता ने पूछा, और मैं यह जोड़ूंगा कि मैंने मूल सूत्रों की सूची में जोड़े गए सूत्र:
\int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C \int{\sin axdx}=-\frac{1}{a}\cos ax+C \int{\cos axdx}=\frac{1}{a}\sin ax+Cसरल प्रतिस्थापन के माध्यम से व्युत्पन्न होते हैं: t=ax
तो, उदाहरण के लिए, जब हमारे पास समाकल हो: \int{{{e}^{-x}}dx} और (प्रोफेसर की प्राथमिकताओं के कारण) सूत्र \int{{{e}^{ax}}dx}=\frac{1}{a}{{e}^{ax}}+C का उपयोग नहीं कर सकते, तो हम प्रतिस्थापन t=-x का उपयोग करते हैं और शांति से गणना जारी रखते हैं।
