जब आप अनिश्चितकालीन इंटीग्रल्स में अपनी गणना के परिणामों की जांच करते हैं, जैसे कि पाठ्यपुस्तक के अंत में दिए गए उत्तरों के साथ, अक्सर आप एक निराशाजनक बिंदु पर पहुँच जाते हैं जहाँ बस “अलग तरह से निकलता है” और आप समझ नहीं पाते कि क्यों।
ये भिन्नताएं कहाँ से आती हैं?
यह जानना महत्वपूर्ण है कि दोनों उत्तर सही हो सकते हैं, यानी आपका और पाठ्यपुस्तक का। पहली बात, एक ही अभिव्यक्ति को विभिन्न तरीकों से लिखा जा सकता है, उदाहरण के लिए:
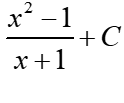
जिसे सरलीकृत करने पर हमें मिलता है:
और उदाहरण के लिए,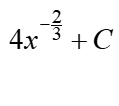 
वही है जो: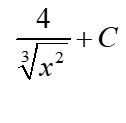 
हालांकि, और अधिक दिलचस्प यह हो सकता है कि परिणाम एक स्थिरांक द्वारा भिन्न हो सकते हैं और इसमें कोई समस्या नहीं है, क्योंकि अनिश्चितकालीन समाकलन परिभाषा के अनुसार फ़ंक्शनों का एक परिवार है जो एक स्थिरांक से भिन्न होता है।
इसलिए:
उसी फ़ंक्शन परिवार का हिस्सा है जैसे:
क्योंकि वे केवल एक स्थिरांक (-1) से भिन्न हैं। दोनों परिणाम सही हैं।
उसी फ़ंक्शन परिवार का हिस्सा भी होगा:
क्योंकि 
एक स्थिरांक है जैसे कि 2 या 3।
