अनंत योग के साथ अनुक्रम की सीमा

आइए निम्नलिखित श्रृंखला की सीमा लें:

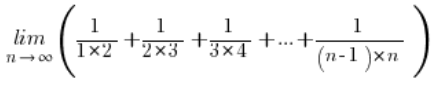
इस समस्या में हमें ऐसा “महसूस” होता है कि हमें श्रृंखला के योग सूत्र (अंकगणितीय या ज्यामितीय) का उपयोग करना चाहिए लेकिन दुर्भाग्य से… यह श्रृंखला न तो अंकगणितीय है और न ही ज्यामितीय…

क्या करें?

हमें इसे पूरी तरह से अलग तरीके से करना होगा। प्रत्येक भिन्न को साधारण भिन्नों में विभाजित करें। यह काफी तीव्रता से किया जाता है जब हम अपरिमेय फलनों के अनिश्चित समाकलनों से निपटते हैं, उदाहरण के लिए। विचार यह है कि A और B स्थिरांक खोजें ताकि…

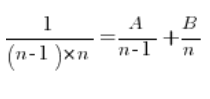
हम उपरोक्त समीकरण के दोनों पक्षों को 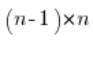से गुणा करते हैं, प्राप्त करते हैं:

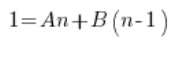
फिर:

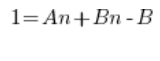
हम बहुपदों के गुणांकों की तुलना करते हैं (बहुपद समानता – हाई स्कूल) और हमें समीकरणों का एक समूह मिलता है:

दूसरे समीकरण से: .

पहले समीकरण में इसे स्थापित करते हुए:

हमें यह भी मिलता है .

तो हम किसी भी भिन्न को विभाजित कर सकते हैं:

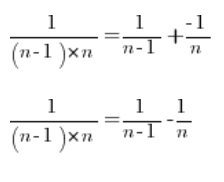
हमारी श्रृंखला की सीमा पर वापस लौटते हुए और प्रत्येक भिन्न को साधारण भिन्नों में विभाजित करते हुए:

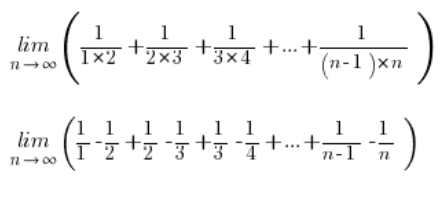
कुछ तत्वों को सरल करते हुए, हमारे पास रह जाता है:

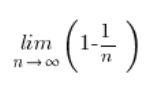
और यह श्रृंखला की सीमा अब डरावनी नहीं है, जाहिर है:

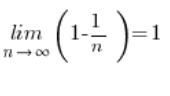
नोट:

श्रृंखला की सीमाओं के कई रोचक उदाहरण आप मेरे वीडियो कोर्स में पा सकते हैं जो सीमाओं को समर्पित है।