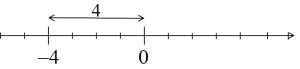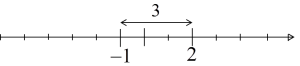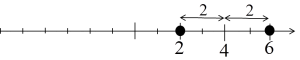अगर आप कुछ समय से विश्वविद्यालय में गणित पढ़ रहे हैं, तो आपने निश्चित रूप से देखा होगा कि स्कूल में पढ़ाई गई अधिकांश सामग्री का विश्वविद्यालय में सीधे तौर पर कोई फायदा नहीं होता। यदि आप अभी-अभी पढ़ाई शुरू कर रहे हैं – इस पर ध्यान दें।
“सीधे तौर पर” का क्या मतलब है?
मैं “सीधे तौर पर” इसलिए कहता हूँ क्योंकि स्पष्ट रूप से आपका हर एक बूंद गणित का पसीना स्कूल में बेकार नहीं जाएगा और आपके लिए गिना जाएगा। मेरा मतलब है अमूर्त सोच में अभ्यास, समस्या पर ध्यान केंद्रित करने की क्षमता आदि।
हालांकि, सीधे तौर पर कहूं तो, आपको स्कूल में पढ़ाए गए गणित के कई भागों की ओर लौटने की जरूरत नहीं पड़ेगी, यहाँ तक कि उन्हें दोबारा देखने के लिए भी नहीं।
लेकिन अपवाद भी हैं।
ऐसी चीजें हैं, जिन्हें स्कूल में पढ़ाया जाता है, जिनके बिना आप विश्वविद्यालय में बहुत दूर तक नहीं जा सकते।
शैक्षणिक वर्ष की शुरुआत में इन्हें दोहराना या बस सीखना उचित रहेगा। इससे आप नए, आगे के विषयों के लिए रास्ता खोलेंगे। यदि इन्हें नहीं सिखाया गया, तो ये लगातार आपको परेशान करेंगे, जैसे जूते में कांटा, और आपकी प्रगति को मुश्किल (या यहां तक कि असंभव) बना देंगे।
ये बड़े गणित के क्षेत्र नहीं होंगे, बल्कि ज्यादातर छोटे विवरण, छोटी ईंटें, जिनके बिना पूरी इमारत गिर सकती है।
सीमा की परिभाषा
उदाहरण के लिए, सीमा अनुक्रम की परिभाषा को लें, जिससे आप बहुत जल्दी सामना करेंगे:
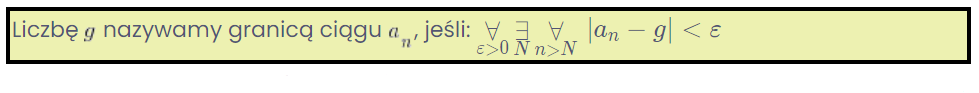
क्या आप बाईं ओर इन अजीब निशानों को समझते हैं? और दाईं ओर इस निरपेक्ष मान को? ज्यादा नहीं?
और फिर भी, इस परिभाषा को समझने या कम से कम सही तरीके से पढ़ने के लिए, क्वांटीफायर (ये जीव बाईं ओर: 
) और निरपेक्ष मान की ज्यामितीय व्याख्या (दाईं ओर) का ज्ञान होना चाहिए, जो कि स्कूल से आता है…
लेकिन हम शिकायत नहीं करेंगे, बल्कि काम शुरू करेंगे। इस और अगले पोस्ट में, मैं आपको कुछ विवरण दिखाऊंगा, जिनके समझने से आपकी विश्वविद्यालय की पढ़ाई बहुत आसान हो जाएगी।
हम शुरू करते हैं…
1. निरपेक्ष मान की ज्यामितीय व्याख्या (दूरी के रूप में)
हम सब आम तौर पर जानते हैं कि इस निरपेक्ष मान का क्या मतलब है। किसी को यह समझने में समस्या नहीं होती कि:
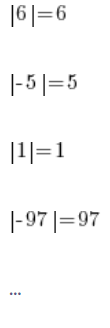
निरपेक्ष मान का ऑपरेशन बस वही संख्या लौटाता है, और यदि वह नकारात्मक है, तो उसके चिह्न को प्लस में बदल देता है।
यह ज्यामितीय रूप से क्या मतलब होगा? संख्या रेखा पर? खैर, बस एक संख्या की शून्य से दूरी। उदाहरण के लिए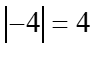 
और वास्तव में, कोई संदेह नहीं, संख्या 
की शून्य से दूरी 4 है:
हम इस रास्ते को और आगे बढ़ाएंगे और निरपेक्ष मान को ठीक उसी तरह समझेंगे जैसे दूरी।
एक और बात पर ध्यान दें:
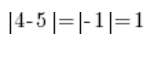
और कि संख्या रेखा पर:
…यानी 4 और 5 के बीच की दूरी ठीक उसी तरह है जैसे 4 और 5 के DIFFERENCE (घटाव) का संख्यात्मक मान, इससे कोई फर्क नहीं पड़ता कि हम किसे किससे घटा रहे हैं, क्योंकि:
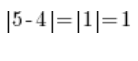
इसी तरह, यदि हम 3 और 8 की संख्याओं को घटाते हैं और परिणाम का निरपेक्ष मान निकालते हैं, तो हमें ठीक 3 और 8 की संख्याओं के बीच की दूरी संख्या रेखा पर मिलेगी (यह 5 होगी)।
यह नकारात्मक संख्याओं पर भी काम करता है, उदाहरण के लिए -1 और 2:
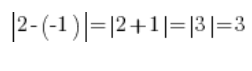
…यानी -1 और 2 की संख्याओं के बीच की दूरी:
आप इसे खुद से भी थोड़ा खेल सकते हैं। अगर आपके पास स्कूल का कोई पाठ्यपुस्तक है, तो मैं आपको दृढ़ता से प्रोत्साहित करता हूँ कि आप इस विषय पर एक घंटे बैठें और इसे थोड़ा छानें।
हम एक सामान्य नियम बना सकते हैं:
दो संख्याओं के अंतर (घटाव) का निरपेक्ष मान: 
और 
इन संख्याओं के बीच की दूरी के बराबर है।
उदाहरण के लिए, हम ऐसी समीकरण को कैसे डिकोड कर सकते हैं:
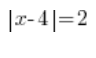
हम जानते हैं कि भाग 
अनजान x से 4 की दूरी का मतलब है, और समानता के दाईं ओर हम जानते हैं कि यह दूरी बराबर होनी चाहिए 2।
तो समीकरण का समाधान वे संख्याएँ होंगी जिनकी दूरी 4 से 2 के बराबर होती है, यानी संख्याएँ 2 और 6:
और अब हम इस असमानता को लेते हैं:
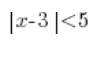
इसका बायाँ हिस्सा x की संख्या 3 से दूरी है, और आगे पढ़ते हुए हमें जानकारी मिलती है कि यह दूरी 5 से कम होनी चाहिए। इस बार इस असमानता का समाधान केवल दो संख्याएँ नहीं होंगी बल्कि और भी बहुत होंगी – सभी संख्याएँ जिनकी दूरी 3 से कम होती है। अक्ष पर यह इस तरह दिखेगा:
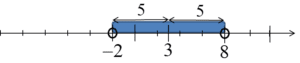
…यानी यह सभी संख्याएँ -2 से 8 तक होंगी, यानी संख्या अंतराल: 
। हर ऐसी संख्या की 3 से दूरी 5 से कम है।
इस संख्या अंतराल को भी एक निश्चित पड़ोस बिंदु 3 के रूप में कहा जा सकता है (एक महत्वपूर्ण शब्दावली, जिसका विश्वविद्यालय में अक्सर उपयोग किया जाता है)।
इसी तरह से सोचते हुए, आप यह पता कर सकते हैं कि कौन सी संख्याएँ असमानता 
…
हालांकि, यह वास्तव में मेरा उद्देश्य नहीं है (आपके पास यह स्कूल में था, है ना 🙂 ?).
निरपेक्ष मान को दूरी के रूप में समझना अच्छा है, क्योंकि यह कई गणितीय परिभाषाओं में आता है, जिनसे आप विश्वविद्यालय में मिलेंगे। और फिर यह तुरंत जानना अच्छा है कि “क्या चल रहा है”।
उदाहरण के लिए, पहले चर्चा की गई अनुक्रम की सीमा लें:
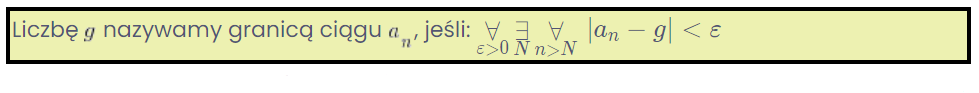
अभी के लिए, हम सूत्र के दाईं ओर ध्यान केंद्रित करेंगे। अगले पोस्ट में बाईं ओर के अजीब निशानों को छोड़ दें।
कौन सी पढ़ाई दिल के करीब आती है और बेहतर समझी जाती है:
“
और 
के बीच का अंतर का निरपेक्ष मान 
से कम होना चाहिए”
या:
“ और के बीच की दूरी से कम होनी चाहिए”
?
औपचारिक रूप से, परिभाषा को बनाने के दोनों तरीके समकक्ष हैं, लेकिन दूसरा सरल है और सार पर ध्यान केंद्रित करता है, बिना किसी जोड़-घटाव के।
निरपेक्ष मान को दूरी के रूप में समझने से आपको विश्वविद्यालय में कई – कथित रूप से जटिल – गणितीय प्रमेयों और परिभाषाओं को समझने में बहुत आसानी होगी।
अब क्या?
अगले पोस्ट में, मैं इन अजीब निशानों से निपटूंगा: 
और 
, ताकि हम अपने उदाहरण की परिभाषा को पूरी तरह से समझ सकें।
