जीवन में कभी-कभी ऐसा होता है कि द्विघातीय समाकल में समाकलन का क्षेत्र दीर्घवृत्त होता है….
तब क्या करें?
दीर्घवृत्तीय निर्देशांक
इसका एक शानदार तरीका आमतौर पर तथाकथित दीर्घवृत्तीय निर्देशांक का उपयोग होता है। यह कुछ ऐसा ही है जैसे ध्रुवीय निर्देशांक, काम करने की प्रक्रिया बिलकुल समान है, बस x और y के लिए आप अलग चीजें रखते हैं और जैकोबियन अलग होता है। ‘r’ की व्याख्या भी अलग है। संक्षेप में, यदि आप ध्रुवीय निर्देशांक पर जा सकते हैं (जो आमतौर पर तब होता है जब समाकलन का क्षेत्र एक वृत्त होता है) तो आप आसानी से दीर्घवृत्तीय निर्देशांक को भी समझ सकते हैं।
तो हमारे पास समाकल है: 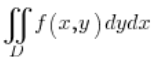 और समाकलन का क्षेत्र जो एक दीर्घवृत्त द्वारा सीमित है, जिसका केंद्र मूल बिंदु पर है और जिसका समीकरण है:
और समाकलन का क्षेत्र जो एक दीर्घवृत्त द्वारा सीमित है, जिसका केंद्र मूल बिंदु पर है और जिसका समीकरण है: 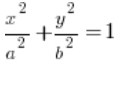 । आइए सुनिश्चित करें कि दीर्घवृत्त समीकरण के दाहिने तरफ निश्चित रूप से 1 हो, ठीक है? अगर उदाहरण के लिए यह 9 है, तो आप इसे 9 से विभाजित करके आसानी से 1 बना सकते हैं।
। आइए सुनिश्चित करें कि दीर्घवृत्त समीकरण के दाहिने तरफ निश्चित रूप से 1 हो, ठीक है? अगर उदाहरण के लिए यह 9 है, तो आप इसे 9 से विभाजित करके आसानी से 1 बना सकते हैं।
आकृत किया गया समाकलन क्षेत्र इस प्रकार दिखता है:
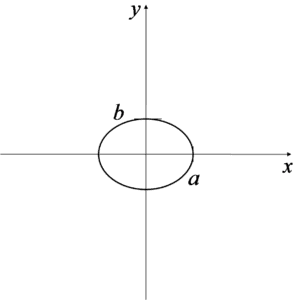
चित्र में a और b का अर्थ हर कोई देख सकता है। ध्यान रखना चाहिए कि अगर दीर्घवृत्त समीकरण के हर में ![]() के नीचे उदाहरण के लिए 9 है, तो इसका मतलब है कि
के नीचे उदाहरण के लिए 9 है, तो इसका मतलब है कि ![]() है, क्यों स्पष्ट है, है ना?
है, क्यों स्पष्ट है, है ना?
अब ऐसी “साफ़” स्थिति होने पर हम दीर्घवृत्तीय निर्देशांक पर जाते हैं, निम्नलिखित को प्रतिस्थापित करते हुए:
![]()
![]()
दीर्घवृत्तीय निर्देशांक में चर का अर्थ
कोण ![]() का अर्थ ध्रुवीय निर्देशांक के समान ही होता है, और
का अर्थ ध्रुवीय निर्देशांक के समान ही होता है, और ![]() का अर्थ अलग होता है। एक सुंदर समीकरण
का अर्थ अलग होता है। एक सुंदर समीकरण 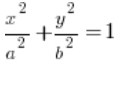 द्वारा दी गई दीर्घवृत्त के बुनियादी समस्याओं में, बस मान लें कि
द्वारा दी गई दीर्घवृत्त के बुनियादी समस्याओं में, बस मान लें कि ![]() शून्य से एक तक बदलता है (अधिक जटिल मामलों में
शून्य से एक तक बदलता है (अधिक जटिल मामलों में ![]() और
और ![]() को दीर्घवृत्त समीकरण में प्रतिस्थापित करें और r की ऊपरी सीमा की गणना करें)।
को दीर्घवृत्त समीकरण में प्रतिस्थापित करें और r की ऊपरी सीमा की गणना करें)।
जैकोबियन
दीर्घवृत्तीय निर्देशांक में जैकोबियन बराबर होता है ![]() ।
।
जैकोबियन को याद रखते हुए हम दीर्घवृत्तीय निर्देशांक में समाकल में जाते हैं:
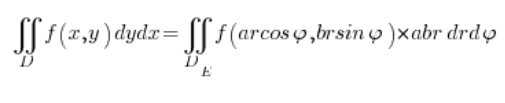
जहां चर ![]() और
और ![]() सीमित होते हैं:
सीमित होते हैं: ![]() शून्य से एक तक की सीमाओं में, और
शून्य से एक तक की सीमाओं में, और ![]() इस पर निर्भर करता है कि हम पूरी दीर्घवृत्त, आधी, या उदाहरण के लिए चौथाई के बारे में बात कर रहे हैं – जैसे कि ध्रुवीय निर्देशांक में।
इस पर निर्भर करता है कि हम पूरी दीर्घवृत्त, आधी, या उदाहरण के लिए चौथाई के बारे में बात कर रहे हैं – जैसे कि ध्रुवीय निर्देशांक में।
बस इसे लें और गणना करें।
उदाहरण
समाकल की गणना करें 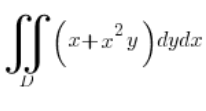 , जहां D एक दीर्घवृत्त है जिसका समीकरण है:
, जहां D एक दीर्घवृत्त है जिसका समीकरण है: 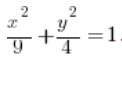 ।
।
उपरोक्त योजना के अनुसार, हम प्रतिस्थापित करते हैं:
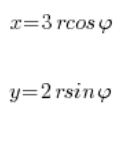
हम समाकलन क्षेत्र को लेते हैं:
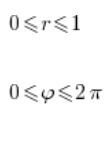
और समाकल की गणना करते हैं:
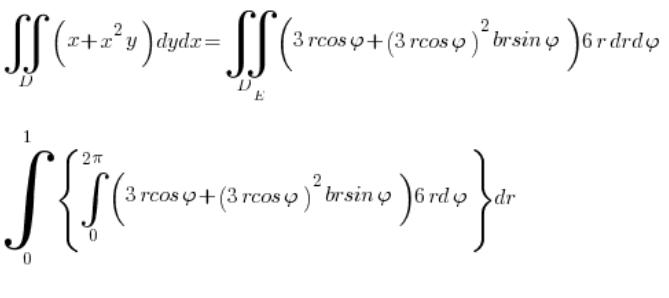
जो अब निश्चित रूप से औपचारिकता मात्र है 🙂