Obliczanie granicy ciągu twierdzeniem o trzech ciągach (VIDEO)
Krystian Karczyński
Założyciel i szef serwisu eTrapez.
Magister matematyki Politechniki Poznańskiej. Korepetytor matematyki z wieloletnim stażem. Twórca pierwszych Kursów eTrapez, które zdobyły ogromną popularność wśród studentów w całej Polsce.
Mieszka w Szczecinie. Lubi spacery po lesie, plażowanie i kajaki.
Na tym filmiku pokazuję, jak obliczyć granicę ciągu zawierającego 
– przy użyciu twierdzenia o trzech ciągach:
Mając do policzenia granicę ciągu z w środku, na przykład:
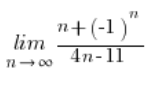
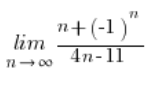
…możemy skorzystać z twierdzenia o trzech ciągach.
Ogólną metodę liczenia granic przy pomocy twierdzenia o trzech ciągach znajdziesz w moim Kursie Granic. W tym poście przedstawię tylko ten jeden, konkretny przypadek ciągu.
Przykład
Wiemy, że liczba będzie zawsze równa liczbie 1 (dla n parzystych), albo -1 (dla n nieparzystych). Prawdą jest więc, że jest zawsze mniejsza lub równa od 1 i większa lub równa od -1, prawda? Prawdziwe są więc nierówności:
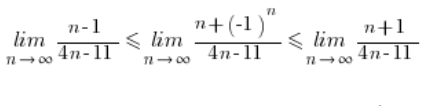
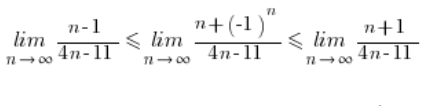
Wyrażenie po prawej ma większy (lub równy) licznik od środkowego, więc całe jest dla dowolnego n większe lub równe od wyrażenia w środku.
Wyrażenie po lewej ma mniejszy (lub równy) licznik od środkowego, więc całe jest dla dowolnego n mniejsze lub równe od wyrażenia w środku.
Teraz pokazujemy, że ciągi ograniczające z góry i z dołu dążą do tej samej granicy (metodami wytłumaczonymi w Kursie Granic):
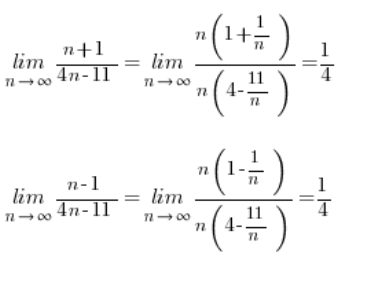
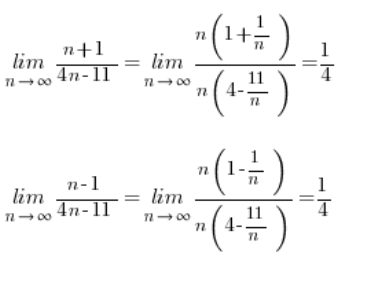
Pokazaliśmy, że ciągi ograniczające z góry i z dołu nasz ciąg wyjściowy dążą do 
, stąd zatem prosty wniosek, że nasza granica ciągu, którą mamy policzyć równa jest (bo tak nam “mówi” twierdzenie o trzech ciągach):
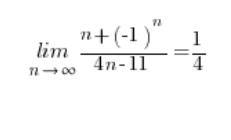
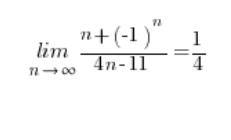
Szukasz korepetycji z matematyki na poziomie studiów lub szkoły średniej? A może potrzebujesz kursu, który przygotuje Cię do matury?
Jesteśmy ekipą eTrapez. Uczymy matematyki w sposób jasny, prosty i bardzo dokładny - trafimy nawet do najbardziej opornego na wiedzę.
Stworzyliśmy tłumaczone zrozumiałym językiem Kursy video do pobrania na komputer, tablet czy telefon. Włączasz nagranie, oglądasz i słuchasz, jak na korepetycjach. O dowolnej porze dnia i nocy.
Chodziło o coś takiego:
?
Bo jeśli tak, to coś tu nie gra, ten ciąg jest rozbieżny, twierdzenie o trzech ciągach nie ma tu zastosowania…
Proszę o pomoc w obliczeniu granicy takiego ciągu przy wykorzystaniu twierdzenia o 3 ciągach: lim (2^n+ (-2)^n)/3^2. Dziękuję.
Witam 🙂 Bardzo proszę o pomoc z taką granicą. Mam w polecaniu powiedziane ze musi to byc policzone metoda o 3 ciagach.
i tak lim przy n –> nieskończoności dalej mam duzy pierwiastek stopnia (n+1) a pod pierwiastkiem n^3 + n^2 + n^1 +1 jest to zadanie z egzaminu
pozdrawiam
ups, przepraszam, nie wyszło 😉 Miała być granica przy n dążącym do nieskończoności i duży pierwiastek n-tego stopnia z 2^n + 2^(-n) +(cos n)^2
Czyli chodzi o taką granicę: \underset{n\to \infty }{\mathop{lim }}\sqrt[n]{{{2}^{n}}+{{2}^{-n}}+{{cos }^{2}}n}[/latex]?
No zasadniczo można pójść na łatwiznę… Z dołu nie ma problemu, prawda?
\sqrt[n]{{{2}^{n}}}\le \sqrt[n]{{{2}^{n}}+{{2}^{-n}}+{{cos }^{2}}n}[/latex]
No i z góry też niewielki problem:
\sqrt[n]{{{2}^{n}}+{{2}^{-n}}+{{cos }^{2}}n}=\sqrt[n]{{{2}^{n}}+\frac{1}{{{2}^{n}}}+{{cos }^{2}}n}\le \sqrt[n]{{{2}^{n}}+1+1}\le \sqrt[n]{{{2}^{n}}+{{2}^{n}}+{{2}^{n}}}[/latex]
No i jesteśmy już w starym schemacie pokazanym w Kursie.
Witam 🙂 Mam pytanie. Muszę obliczyć taką granicę: underset{n\to\infty}{\mathop{lim}},sqrt[n]{2^n + 2^(-n) + (cos n)^2}[/latex]
wydaje mi się, że trzeba to obliczyć z twierdzenia o trzech ciągach. W takim razie jak to ograniczyć? Przez cosinusa mam wątpliwości 😛
Witam 🙂 Mam pytanie a w zasadzie to prosiłbym o radę, mianowicie studiuje na Uniwersytecie Ekonomicznym i na matematyce w zasadzie nie omawialismy zbytnio Granic , zaś jedyne to co omówilismy to takie pojęcia jak :rachunek marginalny (krańcowy) oraz iloraz różnicowy.Na kazde z tych pojęć jest osobny wzór.I własnie chciałbym sie dowiedziec które lekcje z kursu Granice pownienem przerobic aby sie tego nauczyc , mam stosunkowo mało czasu i nie chciałbym się uczyć więcej niz jest mi potrzebne na kolokwium.Z góry dziękuje za odpowiedź
Witam, do tego to bardziej się przyda Kurs Pochodnych, ale ciężko będzie przełożyć pojęcia czysto matematyczne na ekonomiczne, a w Kursie jest tylko czysta matematyka…