Granice ciągu wykorzystują czasami wzory na sumę ciągów arytmetycznego lub geometrycznego. Gorzej jeśli te ciągi podane są w sposób „zmiksowany” w jednej linijce, tak jak tutaj:
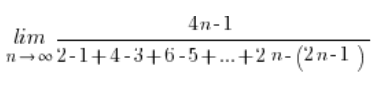
Warto pogrupować inaczej wyrazy w mianowniku, żeby zauważyć, że właściwie są tam dwa ciągi arytmetyczne:
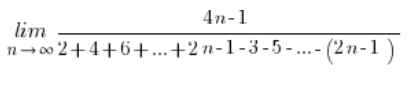
Teraz korzystamy już ze wzorów na sumę:
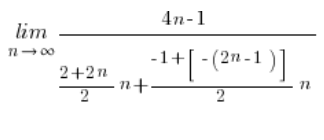
I dalej już tylko liczymy:
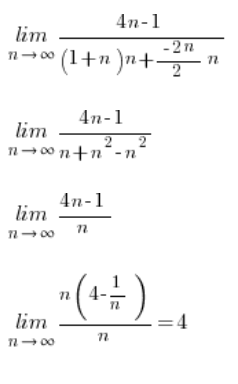
Granica ciągu policzona 🙂
konometria jest dosyć młodą dziedziną wypływającą z ekonomii i matematyki. W praktyce, dzięki modelom ekonometrycznym, możesz „zmierzyć gospodarkę”.Polega to konkretnie na zmierzeniu, jak zachowuje się jedna zmienna w zależności od innych. I na podstawie analizy tego, co było, możesz określać, co będzie się działo w przyszłości.
Wykorzystasz do tego przeróżne obliczenia, testy, schematy. Jedne będą bardzo proste, inne trudniejsze. Jednak najczęściej będzie się liczyło nie to, jak dojdziesz do wyniku, ale jak go zinterpretujesz, odczytasz i jakie wnioski wyciągniesz.
Poniższe Wykłady dotykają najważniejszych pojęć teoretycznych. Jestem przekonana, że pomogę Ci odkrywaniu tego, czym jest ekonometria. I przy okazji uda Ci się zaliczyć ten przedmiot na studiach.
Wirtualny nauczyciel AI działający w przeglądarce internetowej.
2 Komentarzy
Krystian Karczyński
Tak, ma Pan rację. Poprawiłem to, żeby się nikomu nie myliło.
Dzięki!
Mateusz
Witam zauważyłem w drugiej linijce błąd: po cyfrze 6 nie powinno być -5. Piszę o tym bo chwile myślałem skąd to się zabrało. Pozdrawiam.