Jak zrozumieć, czym są funkcje wielu zmiennych?

---

Zrozumienie od samej podstawy, czym właściwie jest funkcja dwóch, albo trzech zmiennych jest dla Ciebie bardzo ważne. Dlaczego, skoro to tylko jeden z wielu działów analizy matematycznej?

Ano dlatego, że na funkcjach wielu zmiennych opiera się mnóstwo rzeczy: pochodne cząstkowe, całki wielokrotne, pół fizyki, trzy czwarte mechaniki i sporo ekonomii.

Funkcja jednej zmiennej – przypomnienie

W edukacji przed szkołą wyższą wprowadzone miałeś pojęcie funkcji jednej zmiennej. Funkcji zależnej od jednego argumentu.

Takimi funkcjami mogły być na przykład:

f\left( x \right)={{x}^{2}} – funkcja przyporządkowuje argumentom  x wartości tych argumentów podniesione do kwadratu. Czyli liczbie 1 przyporządkuje liczbę 1, liczbie 2 liczbę 4, liczbie -3 liczbę 9 itd.

y=x – funkcja przyporządkowuje argumentom  x wartości równe po prostu tym argumentom. Czyli liczbie 1 przyporządkuje liczbę 1, liczbie 2 liczbę 2, liczbie -3 liczbę -3 itd.

Jeżeli umówimy się, że promień koła jest argumentem  r, pole koła jest również funkcją jednej zmiennej (zależy tylko od  r)  P=\pi {{r}^{2}}.  Przyporządkowuje promieniowi 1 pole o wartości około 3,14, promieniowi 2 pole w przybliżeniu 12,56 itd.

Funkcjami jednej zmiennej mogą być również:

• droga w zależności od czasu (argument = czas, wartość = droga)
• przychód w zależności od liczby klientów wchodzących do sklepu (argument = liczba klientów, wartość = przychód)
• ocena z kolokwium w zależności od procentu uzyskanych punktów (argument = procent, wartość = ocena)
• liczba miejsc w parlamencie w zależności od liczby oddanych na nią głosów (argument = liczba głosów, wartość = liczba miejsc)
• zarobki w zależności od wykształcenia (argument = wykształcenie, wartość = zarobki)

Jeżeli chodzi o funkcje liczbowe (liczbom przyporządkowują liczby) poznałeś już zgrabny sposób ich “wizualizacji”, tzn. wykres w 2 wymiarach, z osiami X i Y.

Funkcje dwóch zmiennych

Funkcje dwóch zmiennych – wprowadzenie, przykłady

Jeśli się jednak chwilę zastanowić, to pojęcie funkcji jednej zmiennej wprost domaga się jakiegoś rozszerzenia. W końcu wokół nas mnóstwo jest rzeczy, które zmieniają się w zależności od dwóch czynników, a nie tylko jednego.

Na przykład już głupia objętość walca z gimnazjum zależy od:

• długości promienia jego podstawy
• jego wysokości

… i opisana jest wzorem:  V=\pi {{r}^{2}}H

Wartości V zmieniają się w zależności zarówno od argumentów r, jak i od H. Co więcej, można zauważyć, że takie same przyrosty r i H nie powodują równych przyrostów V. Objętość jest bardziej “wrażliwa” na zmiany promienia podstawy – zwiększanie promienia powoduje szybsze zwiększanie objętości, niż zwiększanie wysokości (przynajmniej przeważnie).

Inne przykłady to:

• opór elektryczny R=\frac{U}{I} zależy od napięcia i natężenia  (argument 1 = napięcie, argument 2 = natężenie, wartość = opór)
• przychód w przedsiębiorstwie w zależności od ceny i ilości sprzedanych towarów  (argument 1 = cena, argument 2 = ilość, wartość = przychód)
• prędkość lotu balonem zależna od siły i kierunku wiatru (argument 1 = siła, argument 2 = kierunek, wartość = prędkość)
• rozmiar kupionego hamburgera w zależności od liczby pieniędzy w kieszeni i stopnia głodu (argument 1 = pieniądze, argument 2 = głód, wartość = rozmiar)
• wysokość składki ubezpieczeniowej OC za samochód w zależności od wieku i ilości stłuczek w ostatnim roku (argument 1 = wiek, argument 2 = ilość stłuczek, wartość = wysokość składki)

Oczywiście, zmianie ulec będzie musiał sposób zaznaczania takich funkcji na wykresie.

Pary argumentów zaznaczyć możemy na płaszczyźnie XY, a na wartości poświęcić kolejną oś, oś Z. Wykres zatem z konieczności musi być trójwymiarowy.

Obejrzyj ten filmik, na którym pokazuję, jak powstaje taki wykres:

Dołączam także parę innych wykresów funkcji dwóch zmiennych:

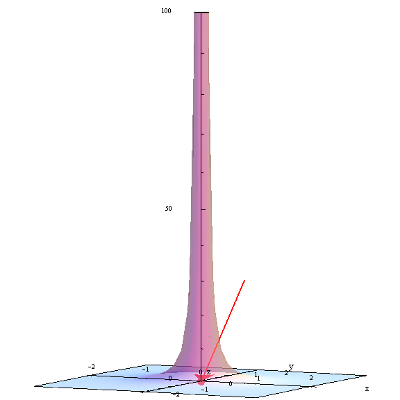
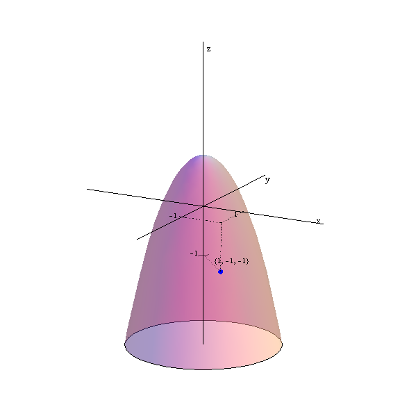
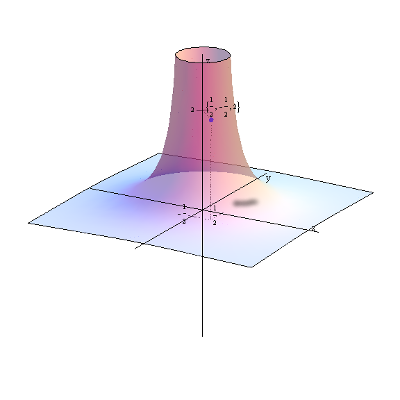
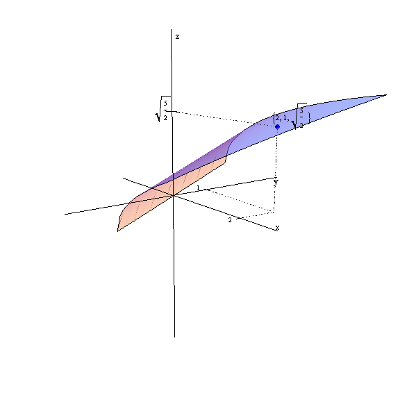
f\left( x,y \right)=1-{{x}^{2}}-{{y}^{2}} z zaznaczoną wartością w punkcie (1,-1): Wykres funkcji f(x,y)=1-x^2-y^2 (paraboloida)	f\left( x,y \right)=\frac{1}{{{x}^{2}}+{{y}^{2}}} z zaznaczoną wartością w punkcie \left( \frac{1}{2},-\frac{1}{2} \right): Wykres funkcji f(x,y)=1/(x^2+y^2) (hiperboloida)
f\left( x,y \right)=x+y-1 z zaznaczoną wartością w punkcie \left( 2,1 \right): Wykres funkcji f(x,y)=x+y-1 (płaszczyzna)	f\left( x,y \right)=\sqrt{x+\frac{y}{2}} z zaznaczoną wartością w punkcie \left( 2,1 \right): Wykres funkcji f(x,y)=sqrt(x+y/2)

Dziedzina (obszar zmienności argumentów) funkcji dwóch zmiennych

Teoria

W przypadku funkcji jednej zmiennej  f\left( x \right)dziedziną tej funkcji był zbiór argumentów x, które w ogóle można do niej podstawić, aby uzyskać jakąś wartość.

Np. do funkcji  f\left( x \right)=\frac{1}{x} można było podstawić za x dowolną wartość z wyjątkiem 0 (bo wtedy było by to dzielenie przez 0), dlatego jej dziedziną był zbiór wszystkich liczb rzeczywistych bez 0 ( R\backslash \left\{ 0 \right\}).

W przypadku funkcji dwóch zmiennych  f\left( x,y \right) dziedziną funkcji w dalszym ciągu będą takie argumenty x,y, które w ogóle można do niej podstawić.

Np. do funkcji  f\left( x,y \right)=\frac{1}{x+y} można podstawić z x i y dowolne wartości, z wyjątkiem takich, dla których y=-x (bo wtedy było by to dzielenie przez zero), dlatego jej dziedziną jest zbiór wszystkich par liczb rzeczywistych (x,y) takich, że  y\ne -x.

Dziedzinę tą można by zaznaczyć na płaszczyźnie zamalowując całą płaszczyznę Z WYJĄTKIEM prostej y=-x.

Praktyka

Dziedzinę funkcji dwóch zmiennych w praktyce wyznaczasz korzystając z tych samych “zastrzeżeń”, co funkcję jednej zmiennej, tzn:

• nie można dzielić przez zero
• pierwiastek można liczyć tylko z liczby nieujemnej
• logarytm można liczyć tylko z liczby dodatniej

Przykład 1

Wyznacz dziedzinę funkcji  f\left( x,y \right)=\frac{1}{{{x}^{2}}+{{y}^{2}}}.

We wzorze na funkcję masz dzielenie. Wiesz, że mianownik w takiej sytuacji musi być różny od zera, zatem zastrzeżenie przyjmie postać:

{{x}^{2}}+{{y}^{2}}\ne 0

{{x}^{2}}+{{y}^{2}} równe jest zero tylko i wyłącznie w przypadku, gdy x i y JEDNOCZEŚNIE są równe zero.

Dziedziną zatem tej funkcji będą wszystkie liczby x i wszystkie liczby y, z wyjątkiem x=0 i y=0.

Wykres 3D funkcji 1/(x^2+y^2). Punkt (0,0) nie należy do dziedziny, więc jest nad nim “dziura”.

Wykres 2D dziedziny funkcji f(x,y)=1/(x^2+y^2). Dziedzina zaznaczona na czerwono.

Przykład 2

Wyznacz dziedzinę funkcji  f\left( x,y \right)=\sqrt{x+y}.

We wzorze na funkcję masz pierwiastek. Wiesz, że argument pierwiastka musi być większy lub równy 0.

Zatem:

x+y\ge 0

Czyli:

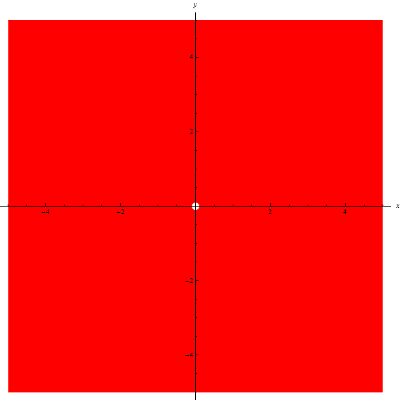
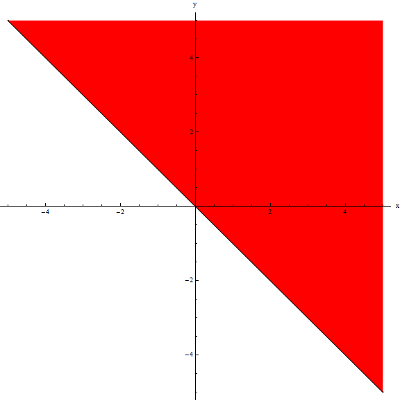
y\ge -x

Dziedziną tej funkcji jest zbiór wszystkich punktów na płaszczyźnie o takich współrzędnych, że  y\ge -x.

Najwygodniej przedstawić to geometrycznie, jako punkty leżące na i nad prostą  y=-x:

Wykres 3D funkcji f(x,y) = sqrt(x+y). DODATKOWO (oprócz wykresu) na płaszczyźnie XY zaznaczyłem dziedzinę.

Dziedzina funkcji y=sqrt(x+y) na płaszczyźnie XY. Obszar na i nad prostą y=-x.

Przykład 3

Wyznacz dziedzinę funkcji  f\left( x,y \right)=\ln \left( y-{{x}^{2}} \right).

Argumentem logarytmu może być tylko liczba dodatnia, zatem:

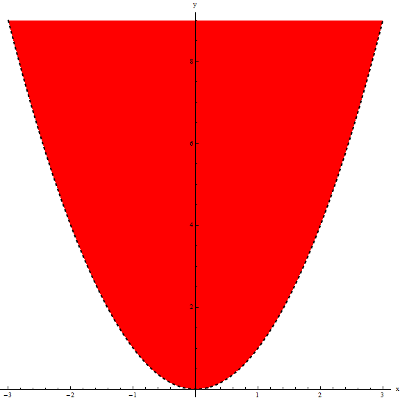
y-{{x}^{2}}>0

Czyli:

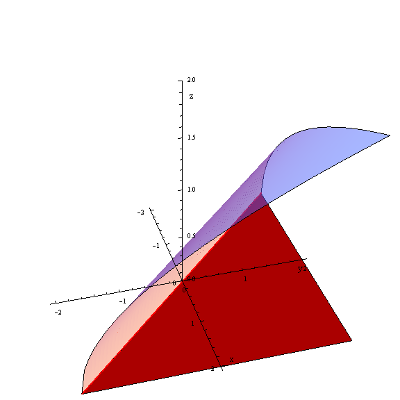
y>{{x}^{2}}

Dziedziną funkcji jest zatem zbiór wszystkich punktów takich, których współrzędne y są większe od współrzędnych x podniesionych do kwadratu. Graficznie będzie to obszar NAD parabolą y={{x}^{2}}, ale BEZ tej paraboli:

Wykres 3D funkcji f(x,y)=ln(y-x^2). Oprócz tego, DODATKOWO na płaszczyźnie XY zaznaczyłem dziedzinę.

Wykres dziedziny funkcji f(x,y)=ln(y-x^2). Dziedzina zaznaczona na czerwono. Sama parabola NIE należy do dziedziny.

Przykład 4

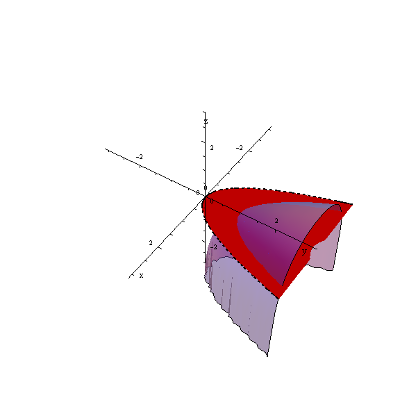
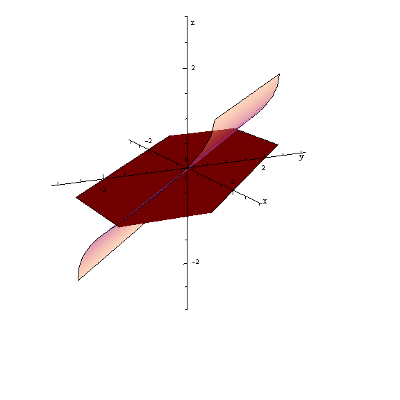
Wyznacz dziedzinę funkcji  z=\arcsin \frac{x+y}{2}.

Arcus sinus jest nieco rzadziej używaną funkcją. Zastrzeżenie co do jego dziedziny jest takie, że argumenty muszą należeć do przedziału  \left\langle -1,1 \right\rangle , zatem:

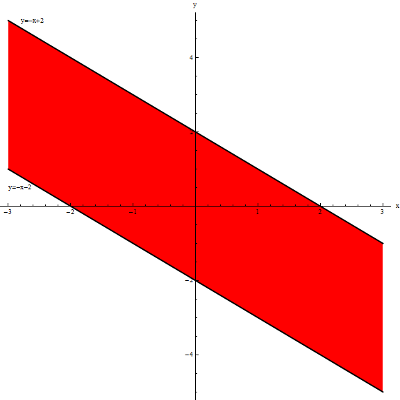
\frac{x+y}{2}\ge -1\quad \wedge \quad \frac{x+y}{2}\le 1 x+y\ge -2\quad \wedge \quad x+y\le 2 y\ge -x-2\quad \wedge \quad y\le -x+2

Dziedziną funkcji będą wszystkie punkty spełniające jednocześnie te dwa warunki. Geometrycznie obszar pomiędzy tymi dwiema prostymi, włącznie z nimi samymi:

Wykres 3D funkcji y=arcsin((x+y)/2). Oprócz niego DODATKOWO na bordowo zaznaczyłem na płaszczyźnie XY dziedzinę.

Dziedzina funkcji arcsin((x+y)/2) na płaszczyźnie XY.

Więcej przykładów Video

Więcej przykładów (także trudniejszych) rozwiązuję i pokazuję krok po kroku na video w moim Kursie Funkcji Wielu Zmiennych . Lekcja 5 Kursu poświęcona jest właśnie liczeniu dziedziny funkcji dwóch zmiennych. Omawiam tam także szerzej cały ogólny schemat wyznaczania dziedziny. Zapraszam, jeśli chcesz bliżej zgłębić ten temat, a także nauczyć się wyznaczać dziedziny, w których jest więcej niż jedno zastrzeżenie (np. dzielenie i pierwiastek w jednej funkcji).

Zadanie domowe

A jeśli chcesz sam się trochę sprawdzić, załączam małe zadanie domowe.

Wyznacz dziedzinę z poniższych funkcji:

1. f\left( x,y \right)=\frac{1}{x+y+3}
2. f\left( x,y \right)=\frac{1}{x-2y}+15xy
3. z=\sqrt{x-y}
4. z=\ln \left( y-2+3x-{{x}^{2}} \right)

 Funkcje trzech i więcej zmiennych

Skoro funkcje jednej zmiennej rozszerzać można na funkcje dwóch zmiennych, nie ma właściwie żadnego logicznego powodu, żeby się na tym zatrzymywać.

Bez problemu wyobrazić sobie można funkcje trzech ( f\left( x,y,z \right)), czterech ( f\left( x,y,z,u \right)) albo w ogóle dowolnej liczby zmiennych ( f\left( {{x}_{1}},{{x}_{2}},\ldots ,{{x}_{n}} \right)).

Z matematycznego punktu widzenia nie ma żadnego problemu, żeby funkcje te badać na takich samych zasadach, co 1 zmiennej. To znaczy liczyć ich granice, pochodne, ekstrema, dziedzinę.

W rzeczywistości jednak pojawia się pewna bariera, związana bardziej z ludzkim postrzeganiem świata, niż matematyką. Chodzi o wykresy.

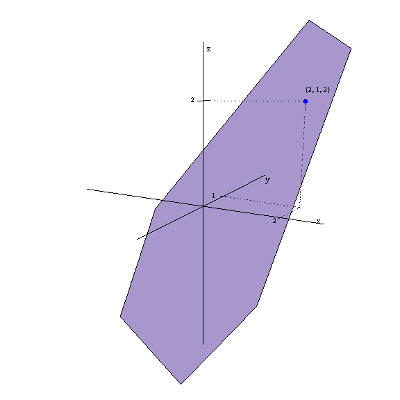
Wyobraźmy sobie funkcję trzech zmiennych  f\left( x,y,z \right)={{x}^{2}}+{{y}^{2}}+{{z}^{2}}. Jej dziedziną jest zbiór trójek argumentów (x,y,z), który możemy przedstawić na trójwymiarowym wykresie. Punkt (1,1,2) jak najbardziej należy do tej dziedziny, bo można go podstawić do funkcji (uzyskując w ten sposób jej wartość:  {{1}^{2}}+{{1}^{2}}+{{2}^{2}}=6).

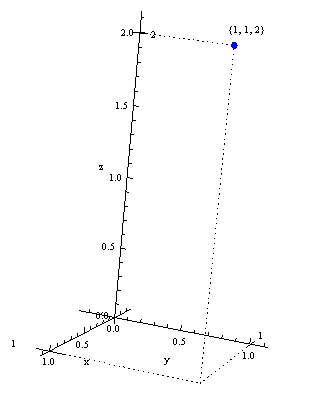
Pytanie jest jednak takie: gdzie zaznaczyć tą wartość funkcji, tzn 6?

Oś ‘z’ służy w tym wykresie do oznaczenia trzeciego argumentu, a nie wartości (tak jak to było w wykresach funkcji dwóch zmiennych).

Aby zaznaczyć jakoś geometrycznie tą wartość musielibyśmy, jak to nieraz się mówi potocznie, jakoś “wejść w czwarty wymiar” i ze zrozumiałych powodów jest to bardzo trudne. Pewnymi pomysłami mogą być tutaj zaznaczenie koloru punkcika (np. im bardziej zimno-niebieski, tym mniejsza wartość, a im bardziej ciepło-czerwony tym większa), ale ich zawodność jest chyba oczywista.

Na funkcjach czterech zmiennych z rysowaniem wykresu wysiadamy już na etapie dziedziny.

To, że nie możemy czegoś narysować, albo zwizualizować choćby w głowie nie oznacza, że nie możemy tego policzyć. Dlatego jeszcze raz podkreślę, że jedyny problem z funkcjami o większej niż 2 liczbie zmiennych jest w ich reprezentacji geometrycznej.

Następny Wykład

Wiesz już, czym są funkcje wielu zmiennych i jak można je sobie “wyobrazić”. Wiesz także, kiedy ich “wyobrazić” sobie nie można 🙂

Przechodzimy zatem do ich dalszej analizy. Pamiętasz z funkcji jednych zmiennych, co było po dziedzinie funkcji i zapoznaniu się z jej wykresem? Tak, tak, dokładnie. Granice.

Pisząc ten post korzystałem z…

1. “Rachunek różniczkowy i całkowy. Tom I.” G.M. Fichtenholz. Wyd. 1966.