Sustitución de Euler del Primer Tipo (para a>0) – Revisión
En el post anterior:
Sustitución de Euler del Primer Tipo
nos ocupamos de integrales del tipo:
,
donde a>0.
También resolvimos una integral de ejemplo que cumple con esta condición, es decir,
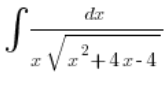
Pero, ¿qué pasa si 
en el trinomio es negativo (se puede omitir el caso cuando a=0 porque entonces no será un trinomio cuadrático y la integral se resolverá por una sustitución más simple 
que la sustitución de Euler)?
Entonces, la segunda clase de sustitución de Euler puede ayudarnos (pero no necesariamente…):
Sustitución de Euler del Segundo Tipo (para c>0)
Teniendo una integral del tipo:
,
en la que c>0, aplicamos una sustitución del tipo:
,
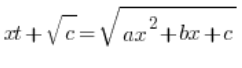la cual volvemos a elevar al cuadrado en ambos lados, donde esta vez los términos con 
se cancelan y que hay que dividir ambos lados por 
para llegar a una relación lineal, de la cual determinaremos con la ayuda de la variable 
en orden:
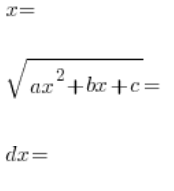
Sustituimos todo esto en la integral:
y obtenemos de nuevo una integral racional, que – repito – generalmente es tediosa.
Empecemos con un ejemplo.
Ejemplo
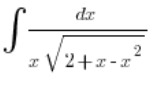
En el trinomio cuadrático, el orden de los términos está ligeramente cambiado, pero está claro que 
. Es decir, que no es mayor que 
(no usaremos entonces la sustitución del primer tipo de Euler), pero c>0 (entonces usaremos el segundo tipo).
Entonces sustituimos:
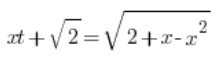
Elevamos ambos lados al cuadrado:
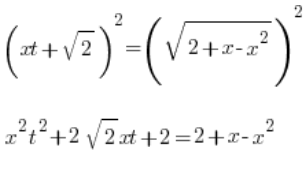
El término 2 se cancela (como debería):
y ahora algo que no estaba en la sustitución del primer tipo, dividimos ambos lados por x:
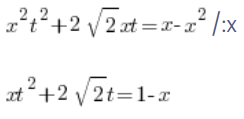
Luego determinamos x:
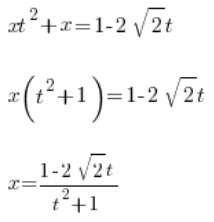
Hemos determinado x con la ayuda de la variable t. Ahora determinamos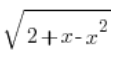 
. Al principio teníamos la sustitución:
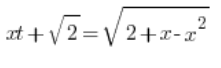
ya está determinado, así que solo lo insertamos:
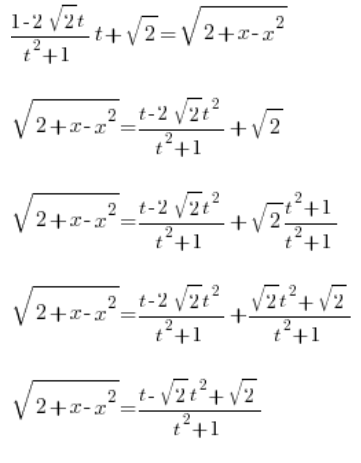
Nos queda determinar solo 
. Lo calculamos derivando :
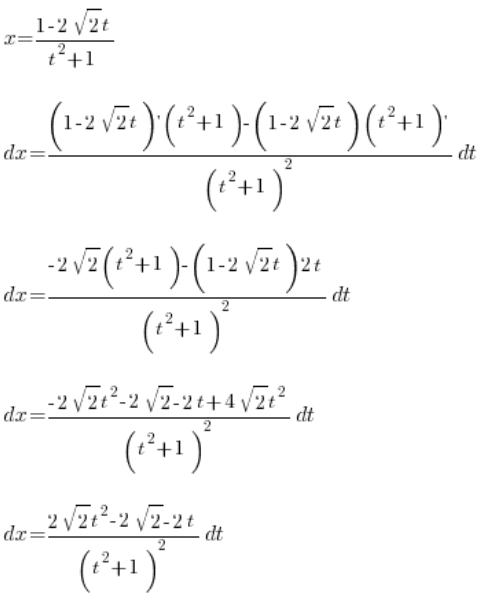
Entonces hemos determinado:
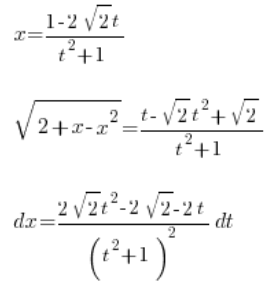
, todo con la ayuda de la variable . Tomamos la integral:
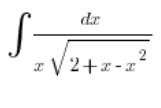
e insertamos:
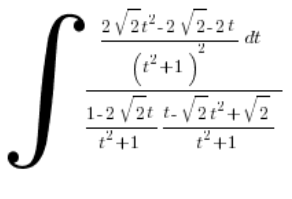
Nos ponemos a limpiar:
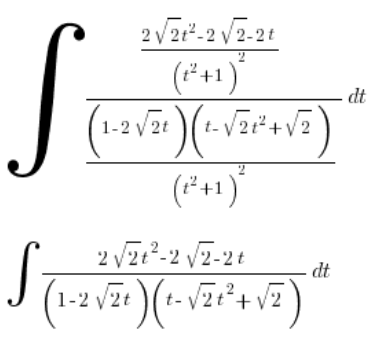
Volviendo a la sustitución:
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+CTodavía tenemos que regresar de t a x. Nuestra sustitución de Euler fue
xt+\sqrt{2}=\sqrt{2+x-{{x}^{2}}}De donde
t=\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x}Entonces nuestra solución es
\frac{1}{\sqrt{2}}\ln \left| u \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}t \right|+C=\frac{1}{\sqrt{2}}\ln \left| 1-2\sqrt{2}\frac{\sqrt{2+x-{{x}^{2}}}-\sqrt{2}}{x} \right|+C¿Qué pasa con otros casos?
Sabemos que cuando en la integral:
- a>0 – usamos la primera clase de sustituciones
- c>0 – usamos la segunda clase de sustituciones
Pero, ¿qué pasa si ni ni son mayores que cero? Lo discutiremos en el próximo post, donde trataré la tercera clase de sustituciones de Euler y mostraré que el tema estará agotado, es decir, para cada tipo de integral:
…elegiremos una de las tres clases de sustituciones.
