Hay días en los que simplemente nada sale bien.
Y hay ejemplos con números complejos en los que nada funciona. Los métodos conocidos y memorizados no ayudan.
Tomemos, por ejemplo, esta potenciación aparentemente inocente:
{( 1+2i )^8}Siguiendo el camino ya recorrido en muchos ejemplos, quieres escribir el número 
en forma trigonométrica y luego elevarlo a la octava potencia usando la fórmula apropiada.
Así que calculas el módulo:
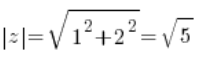
Calculas el seno y el coseno del argumento principal:
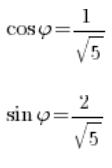
Las señales del coseno y el seno son positivas, por lo que el ángulo está en el primer cuadrante, pero tu suerte termina aquí.
Desafortunadamente, los valores del seno y el coseno: 
y 
no se encuentran en la tabla de valores trigonométricos básicos. No es de extrañar – el ángulo 
no es ni 0, ni 30, ni 45, ni 60, ni 90 grados.
Así que tenemos un PROBLEMA.
¿Qué se puede hacer?
Situaciones en las que un número elevado a una potencia no se puede convertir fácilmente en forma trigonométrica pueden ocurrir. Desafortunadamente.
Pero nadie dijo que el mismo número ELEVADO AL CUADRADO (por ejemplo) seguirá siendo «inconvertible».
Así que inténtalo:
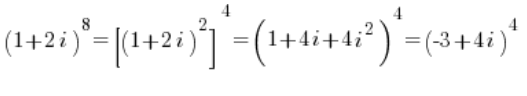
En lugar de convertir el número: 
en forma trigonométrica, conviertes el número 
…
Desafortunadamente, con un resultado igualmente malo, porque aunque el módulo sea bonito y redondo, los valores del seno y el coseno aún no se pueden leer de la tabla.
¿Qué ahora?
Repite la maniobra 🙂
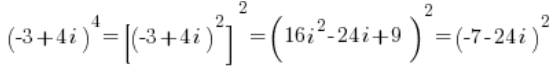
Y aquí, en lugar de luchar con la forma trigonométrica, simplemente elévalo al cuadrado en forma algebraica:
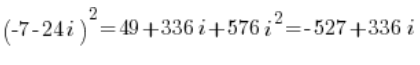
De esta manera, fíjate, sin tocar realmente la forma trigonométrica (porque no se podía), hemos calculado una potencia relativamente alta del número complejo de manera bastante – creo que aún sin dolor -:
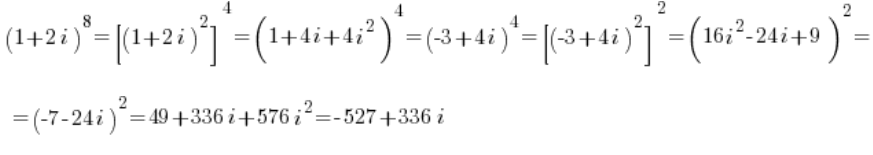
Por supuesto. Esto no siempre «funciona». Pero puede ayudar a veces, ¿verdad? 🙂
