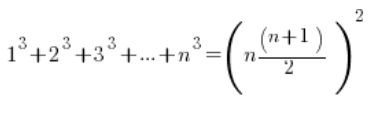No hay productos en el carrito.
Krystian Karczyński- 5 agosto 2024
- Komentarz 0
A veces, en los límites de las sucesiones, pasa algo así:
y a veces incluso así:
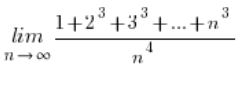
¿Qué hacemos entonces?
La respuesta es simple:
fórmulas para la suma de cuadrados y la suma de cubos de los números naturales consecutivos.
Van así:
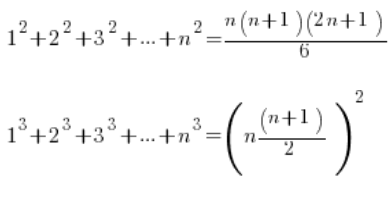
Las fórmulas – como todas las fórmulas – son para memorizar. Si has tenido ejemplos similares y realmente los necesitas.
Conociendo estas fórmulas, calcular nuestros límites se vuelve trivial:
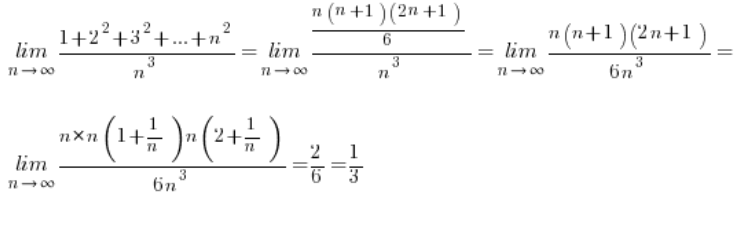
Siguiente límite:
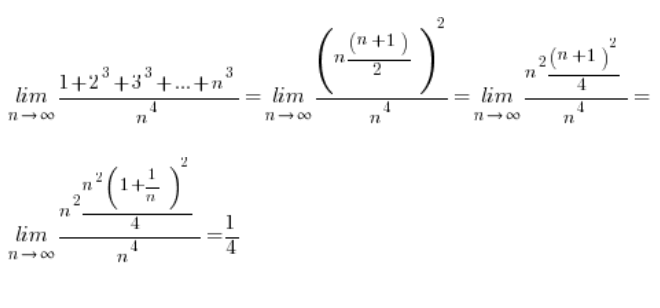
Pruebas inductivas para fórmulas
La validez de las fórmulas se puede demostrar bastante fácilmente de manera inductiva (al menos hace unos años esto era un estándar completo en la escuela secundaria). Lo haré para la fórmula:
1. 
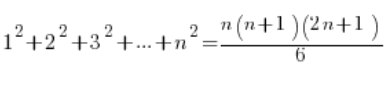
Paso 1 de la inducción
Verificamos la validez de la fórmula para n=1:
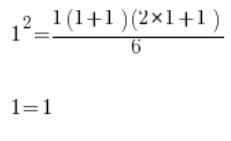
Coincide
Paso 2 de la inducción
Asumimos suposición, que para un cierto n natural:
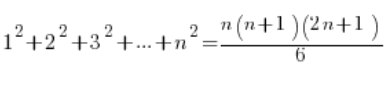
Paso 3 de la inducción
Demostramos la tesis (usando la suposición aceptada), que para n+1 la fórmula también se cumple, es decir:
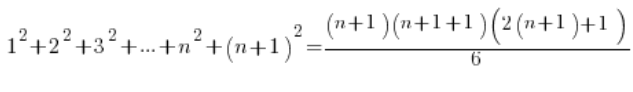
En el lado izquierdo en lugar de 
colocamos la fórmula de la suposición, en el lado derecho solo organizamos:
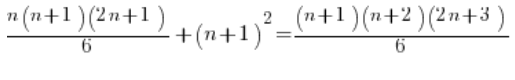
Y luego, en lugar de forzarlo, trabajamos un poco más sutilmente:
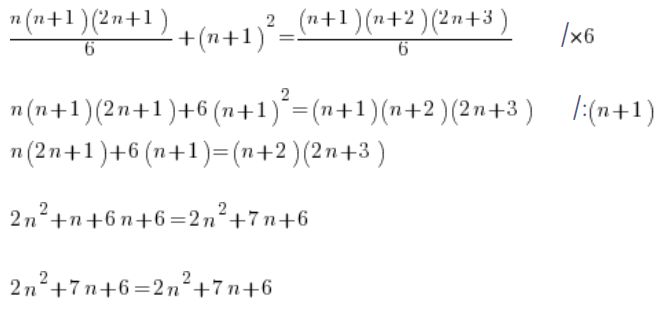
Entonces, la tesis está probada. La fórmula está demostrada inductivamente.
Te invito a demostrar inductivamente la segunda fórmula, para la suma de cubos:
