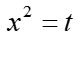En integrales racionales indefinidos, como sabemos, a menudo es necesario descomponer el denominador de la función a integrar en factores y descomponerlo aún más en fracciones simples.
Sin embargo, la descomposición en factores en sí misma puede ser a menudo problemática.
Situaciones típicas
Para situaciones simples como:
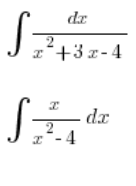
Podemos manejarlas:
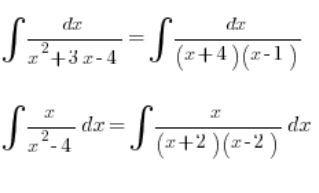
Si el denominador es un polinomio de tercer grado adecuadamente «arreglado», también podemos manejarlo:
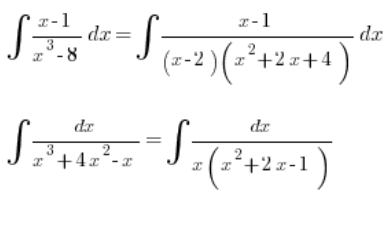
Denominador con un polinomio de tercer grado no amigable
El problema comienza cuando el denominador tiene un polinomio de tercer grado más «no amigable» para descomponer, por ejemplo:
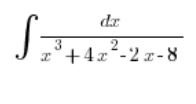
Respira profundo.
Controla el pánico.
Estas cosas (descomposición de este tipo de polinomio) se hacían ya en la escuela secundaria y a nivel básico.
Sólo necesitas un truco ingenioso:
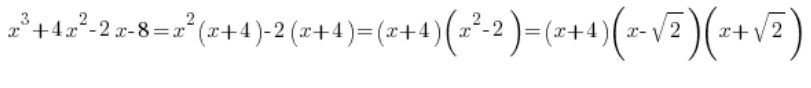
¿Recuerdas? Claro que sí…
Entonces podemos descomponer el polinomio en el denominador:
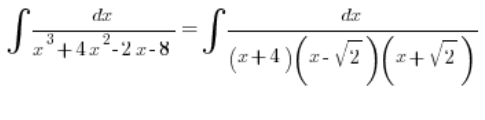
Y luego alegremente descomponerlo en tres fracciones simples, como nos dicen las reglas.
Descomposición aún más difícil
¿Y qué tal esta situación? ¿Recuerdas de la secundaria (esto ya es más avanzado)?
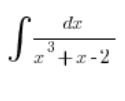
Aquí era un poco peor. El término medio tenía que descomponerse en dos:
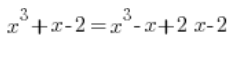
Y luego proceder como de costumbre:
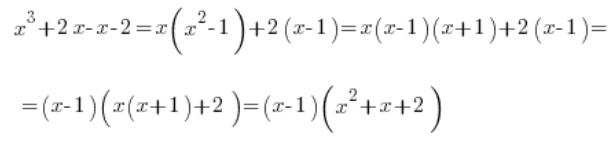
Es decir, la integral debe escribirse como:
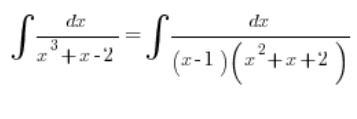
Y seguir calculando con calma.
Métodos de descomposición del denominador en factores en integrales racionales
En general, recuerda en integrales racionales que si es necesario descomponer el polinomio en factores, todos los trucos de la secundaria están permitidos, y pueden incluir, por ejemplo:
- Descomposición de algunos polinomios de cuarto grado mediante sustitución auxiliar

- Buscar «a ciegas» una raíz y dividir el polinomio para reducir su grado
Por supuesto, ahora solo estamos hablando de las integrales racionales indefinidas más difíciles, que en muchas (¿la mayoría?) universidades ni siquiera se introducen!